题目内容
16.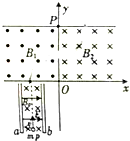 如图所示,纸面内有直角坐标系xOy,在第一,二象限y≤p的区域内分别存在垂直于纸面的匀强磁场B1,B2,方向相反,在第三象限有一速度选择器,a,b板与x轴垂直,板间匀强电场E和匀强磁场B0相互垂直,现有一质量为m,电荷量大小为q的粒子能够沿直线通过速度选择器,并垂直于x轴射入磁场B1,并最终从第一象限y=p上的某点垂直射出磁场B2,已知粒子始终在纸面内运动,且每次均垂直越过y轴进入磁场,不计粒子重力.
如图所示,纸面内有直角坐标系xOy,在第一,二象限y≤p的区域内分别存在垂直于纸面的匀强磁场B1,B2,方向相反,在第三象限有一速度选择器,a,b板与x轴垂直,板间匀强电场E和匀强磁场B0相互垂直,现有一质量为m,电荷量大小为q的粒子能够沿直线通过速度选择器,并垂直于x轴射入磁场B1,并最终从第一象限y=p上的某点垂直射出磁场B2,已知粒子始终在纸面内运动,且每次均垂直越过y轴进入磁场,不计粒子重力.(1)求粒子的电性及进入磁场B1时的速度;
(2)写出p的表达式
(3)用p,E,B0表示粒子在磁场中运动的时间.
分析 (1)根据粒子在磁场中的偏转方向判断出洛伦兹力方向,然后应用左手定则判断粒子电性,由平衡条件求出粒子的速度.
(2)粒子在磁场中做匀速圆周运动,由牛顿第二定律求出粒子轨道半径,然后求出p的表达式.
(3)根据粒子在磁场中做圆周运动的周期求出粒子在磁场中的运动时间.
解答 解:(1)由题意可知,粒子进入第二象限后向右偏转,然后进入第一象限,
粒子进入第二象限后向右偏转,刚进入第二象限时所受洛伦兹力水平向右,
由左手定则可知,粒子带正电,粒子在速度选择器中做匀速直线运动,
由平衡条件得:qvB0=qE,则粒子速度:v=$\frac{E}{{B}_{0}}$;
(2)由题意可知,粒子在磁场中的运动轨迹如图所示: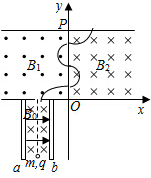
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,r=$\frac{mv}{qB}$=$\frac{mE}{qB{B}_{0}}$,
则粒子在两磁场中的轨道半径:r1=$\frac{mE}{q{B}_{1}{B}_{0}}$,r2=$\frac{mE}{q{B}_{2}{B}_{0}}$,
如图示运动轨迹,由几何知识可得:
p=r1+2n(r1+r2)+r2=(2n+1)($\frac{mE}{q{B}_{1}{B}_{0}}$+$\frac{mE}{q{B}_{2}{B}_{0}}$) n=0、1、2、3、…
(3)粒子在磁场中做圆周运动的周期:T=$\frac{2πr}{v}$=$\frac{2πm}{qB}$,
则:T1=$\frac{2πm}{q{B}_{1}}$,T2=$\frac{2πm}{q{B}_{2}}$,粒子在第一、二象限磁场中的运动时间:
t=$\frac{1}{4}$(T1+T2)+n×$\frac{1}{2}$(T1+T2)=$\frac{1+2n}{4}$($\frac{2πm}{q{B}_{1}}$+$\frac{2πm}{q{B}_{2}}$)=$\frac{2π(1+2n)}{4}$($\frac{m}{q{B}_{1}}$+$\frac{m}{q{B}_{2}}$)=$\frac{πp{B}_{0}}{2E}$;
答:(1)粒子带正电,进入磁场B1时的速度为$\frac{E}{{B}_{0}}$;
(2)p的表达式为:p=(2n+1)($\frac{mE}{q{B}_{1}{B}_{0}}$+$\frac{mE}{q{B}_{2}{B}_{0}}$) n=0、1、2、3、…;
(3)粒子在第一二象限磁场中运动的时间为$\frac{πp{B}_{0}}{2E}$.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程,应用牛顿第二定律、粒子周期公式即可正确解题,处理粒子在磁场中的问题要作出粒子的运动轨迹.

 阅读快车系列答案
阅读快车系列答案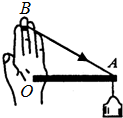 如图所示,用一根细绳和一根轻直杆组成三角支架,绳的一端绕在手指上B点,杆的一端顶在掌心O处,当在A处挂上重物时,整个系统处于静止状态,此时杆OA处于水平状态,绳与杆分别对手指和手掌有力的作用,对这两个作用力的说法正确的是( )
如图所示,用一根细绳和一根轻直杆组成三角支架,绳的一端绕在手指上B点,杆的一端顶在掌心O处,当在A处挂上重物时,整个系统处于静止状态,此时杆OA处于水平状态,绳与杆分别对手指和手掌有力的作用,对这两个作用力的说法正确的是( )| A. | 绳对手指的拉力沿AB方向(与图示方向相反) | |
| B. | 杆对手掌的拉力沿OA方向 | |
| C. | 绳子对A点的作用力和杆对A点的作用力的合力大小大于重物的重力 | |
| D. | 绳子对A点的作用力和杆对A点的作用力的合力方向竖直向上 |
| A. | $\frac{vt}{2}$ | B. | vt0(1-$\frac{{t}_{0}}{2t}$) | C. | $\frac{vt_0^2}{2t}$ | D. | $\frac{{v{{(t-{t_0})}^2}}}{2t}$ |
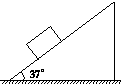 如图所示,在倾角为37°的固定斜面上,放置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8.已知sin37°=0.6,cos37°=0.8,g=10m/s2.
如图所示,在倾角为37°的固定斜面上,放置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8.已知sin37°=0.6,cos37°=0.8,g=10m/s2.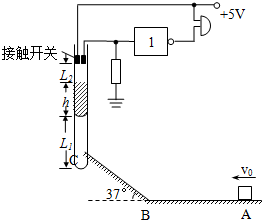 如图所示为一简易火灾报警装置.其原理是:开口向上竖直放置的试管中装有水银,内有接触开关(厚度不计),只要有水银浸没,它就会导通,蜂鸣器发出报警的响声.27℃时,空气柱长度L1为30cm,水银上表面与接触开关下端的距离L2为10cm,管内水银柱的高度h为25cm,外界大气压强为75cmHg.求:
如图所示为一简易火灾报警装置.其原理是:开口向上竖直放置的试管中装有水银,内有接触开关(厚度不计),只要有水银浸没,它就会导通,蜂鸣器发出报警的响声.27℃时,空气柱长度L1为30cm,水银上表面与接触开关下端的距离L2为10cm,管内水银柱的高度h为25cm,外界大气压强为75cmHg.求: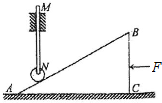 有一重力为2000N的竖直杆MN限制在如图所示的卡槽中,只能沿竖直方向运动,它跨斜面接触端装一轻质滑轮,斜面AB长5m,高BC长3m,在BC边加一水平推力F使斜面体沿水平方向匀速运动(不考虑一切摩擦).求推力F的大小是多少?
有一重力为2000N的竖直杆MN限制在如图所示的卡槽中,只能沿竖直方向运动,它跨斜面接触端装一轻质滑轮,斜面AB长5m,高BC长3m,在BC边加一水平推力F使斜面体沿水平方向匀速运动(不考虑一切摩擦).求推力F的大小是多少?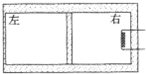 如图所示,一个密闭的气缸,被不导热的光滑活塞分成体积相等的左右两室,气缸壁的左侧导热,其它部分不导热.开始时,两部分气体的体积、温度和压强都相同.现利用右室中的电热丝对右室中的气体加热一段时间,达到平衡后,左室的体积变为原来体积的$\frac{3}{4}$.已知外界环境温度为300K,求平衡后右室气体的温度.
如图所示,一个密闭的气缸,被不导热的光滑活塞分成体积相等的左右两室,气缸壁的左侧导热,其它部分不导热.开始时,两部分气体的体积、温度和压强都相同.现利用右室中的电热丝对右室中的气体加热一段时间,达到平衡后,左室的体积变为原来体积的$\frac{3}{4}$.已知外界环境温度为300K,求平衡后右室气体的温度. 如图所示,在倾角为θ的固定光滑绝缘斜面上,有一劲度系数为k的长绝缘轻质弹簧,其下端固定于斜面底端,上端与一质量为m,带正电的小球A相连,整个空间存在一平行于斜面向上的匀强磁场,小球A静止时弹簧恰为原长.另一质量也为m的不带电的绝缘小球B从斜面上的P点由静止开始下滑,与A发生碰撞后一起沿斜面向下运动,碰撞时间极短,且不粘连.在以后的运动过程中,A与B左所能达到的最高点恰未分开.全过程中小球A的电量不发生变化,弹簧形变始终在弹性限度内,重力加速度为g.求:
如图所示,在倾角为θ的固定光滑绝缘斜面上,有一劲度系数为k的长绝缘轻质弹簧,其下端固定于斜面底端,上端与一质量为m,带正电的小球A相连,整个空间存在一平行于斜面向上的匀强磁场,小球A静止时弹簧恰为原长.另一质量也为m的不带电的绝缘小球B从斜面上的P点由静止开始下滑,与A发生碰撞后一起沿斜面向下运动,碰撞时间极短,且不粘连.在以后的运动过程中,A与B左所能达到的最高点恰未分开.全过程中小球A的电量不发生变化,弹簧形变始终在弹性限度内,重力加速度为g.求: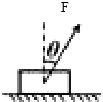 一质量为1kg的物块置于水平地面上.现用一个水平恒力F 拉物块,一段时间后撤去恒力F,已知从物体开始运动到停止,经历的时间为4s,运动的位移为10$\sqrt{3}$m物体与地面间的动摩擦因数为$\frac{\sqrt{3}}{3}$.(g=10m/s2)
一质量为1kg的物块置于水平地面上.现用一个水平恒力F 拉物块,一段时间后撤去恒力F,已知从物体开始运动到停止,经历的时间为4s,运动的位移为10$\sqrt{3}$m物体与地面间的动摩擦因数为$\frac{\sqrt{3}}{3}$.(g=10m/s2)