题目内容
8．
如图所示，半径为R的光滑半圆形轨道CDE在竖直平面内与光滑水平轨道AC相切于C点，水平轨道AC上有一轻质弹簧，弹簧左端连接在固定的挡板上．现用一个小球将弹簧压缩（不栓接），当弹簧的压缩量为l时释放质量为m的小球．小球在运动过程中恰好通过半圆形轨道的最高点E，再次在B点用该小球压缩弹簧，当弹簧的压缩量为2l时释放小球，小球再次沿轨道运动到E点．试求小球第二次到达轨道最高点E时，小球与轨道间的相互作用力F的大小．已知弹簧压缩时弹性势能与压缩量的二次方成正比，弹簧压缩时始终处在弹性限度内．
分析 根据牛顿第二定律求得第一次在E的速度，然后由动能定理求得弹性势能；再根据弹性势能和压缩量的关系求得第二次弹性势能，即可由动能定理求得在E点的速度，最后由牛顿第二定律求得作用力．
解答 解：当弹簧的压缩量为l时释放质量为m的小球．小球在运动过程中恰好通过半圆形轨道的最高点E，那么对小球在E点应用牛顿第二定律可得：$mg=\frac{m{{v}_{E1}}^{2}}{R}$；
对小球运动到E的过程应用动能定理可得：${E}_{p1}-2mgR=\frac{1}{2}m{{v}_{E1}}^{2}=\frac{1}{2}mgR$
解得：${E}_{p1}=\frac{5}{2}mgR$；
当弹簧的压缩量为2l时，由弹簧压缩时弹性势能与压缩量的二次方成正比可知弹性势能为：
${E}_{p2}={2}^{2}{E}_{p1}=10mgR$；
那么，对小球运动到E的过程应用动能定理可得：${E}_{p2}-2mgR=\frac{1}{2}m{{v}_{E2}}^{2}$
解得：${v}_{E2}=4\sqrt{gR}$；
故对小球在E点应用牛顿第二定律可得：$F+mg=\frac{m{{v}_{E2}}^{2}}{R}=16mg$
所以，小球第二次到达轨道最高点E时，小球与轨道间的相互作用力F的大小F=15mg；
答：小球第二次到达轨道最高点E时，小球与轨道间的相互作用力F的大小为15mg．
点评 经典力学问题一般先对物体进行受力分析，求得合外力及运动过程做功情况，然后根据牛顿定律、动能定理及几何关系求解．
练习册系列答案
相关题目
14．如图所示是某电场中的一条电场线．A、B两点处的电势分别为φA、φB．则下列判断正确的是（ ）
| A． | φA＞φB | B． | φA＜φB | C． | φA=φB | D． | 无法比较 |
12．实验表明，可见光通过三棱镜时各色光的折射率n随着波长λ的变化符合科西经验公式：n=A+$\frac{B}{{λ}^{2}}$+$\frac{C}{{λ}^{4}}$，其中A、B、C是正的常量．太阳光进入三棱镜后发生色散的情形如图所示．则（ ）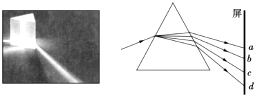
| A． | 屏上d处是紫光 | |
| B． | 屏上d处的光在棱镜中传播速度最大 | |
| C． | 屏上a处是紫光 | |
| D． | 屏上a处的光在棱镜中传播速度最小 |
如图所示，滑块和小球由一不可伸长的轻绳相连，质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，轻绳长为L，开始时，轻绳处于水平拉直状态，小球和滑块均静止，现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有黏性物质的固定挡板P粘住，在极短的时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向的夹角θ=60°时小球到达最高点．求：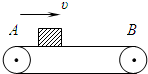
如图所示，水平传送带以v=2m/s的速度匀速运动，A、B两点相距s=11m，一质量m=1kg的物块（可视为质点）从A点由静止开始运动．已知物块与传送带间的动摩擦因数μ=0.2，重力加速度g=10m/s2．
如图所示，AB是倾角为θ=30°的粗糙直轨道，BCD是光滑的圆弧轨道，AB恰好在B点与圆弧相切，圆弧的半径为R，一个质量为m的物体（可以看做质点）从直轨道上的P点由静止释放，结果它能在两轨道间做往返运动．已知P点与圆弧的圆心O等高，物体做往返运动的整个过程中在AB轨道上通过的路程为s．求：
17．一α粒子与一质量数为A（A＞4）的原子核发生弹性正碰．若碰前原子核静止，则碰撞前与碰撞后α粒子的速率之比为（ ）
| A． | $\frac{A-4}{A+4}$ | B． | $\frac{{{{（A+4）}^2}}}{{{{（A-4）}^2}}}$ | C． | $\frac{4A}{{{{（A+4）}^2}}}$ | D． | $\frac{A+4}{A-4}$ |
