题目内容
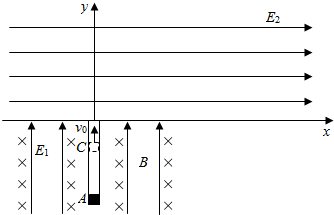
3.如图所示,在竖直平面xOy内,x轴的下方存在匀强电场E1和磁感应强度大小B=0.02T的匀强磁场,电场竖直向上,磁场的方向垂直纸面向里.在x轴的上方空间存在电场强度大小E2=0.075N/C,方向水平向右的匀强电场.有一粗糙的方口塑料直管置于y轴上,长为3m,其开口端正好位于坐标原点O处,一质量m=4×10-6kg,电荷量q=4×10-4C的带电小滑块(尺寸比管口边长略小)自塑料直管A处,由静止开始运动,当运动到离管口1m处的C点时已达到最大速度v0=5m/s,并最终从管口射出.已知小滑块与直管间动摩擦因数μ=0.5,重力加速度g=10m/s2.(1)求电场强度的大小E1.
(2)求小滑块从A点开始运动到原点O的过程中克服摩擦力做的功.
(3)求小滑块从管口射出后的最小速度.
分析 (1)速度最大时加速度为0,合力为0,根据受力平衡求E1;
(2)根据动能定理求克服摩擦力做功;
(3)根据运动的合成与分解,速度最小时合力与速度垂直,根据运动学公式和牛顿定律求解.
解答 解:(1)在塑料管中从A点静止释放,到C点达到最大速度,C点加速度为0,合力为0,
水平方向:FN=qv0B①;
竖直方向:E1q-f-mg=0②;
其中:f=μFN③;
联立①②③解得:E1=$\frac{μq{v}_{0}B+mg}{q}$=$\frac{0.5×4×1{0}^{-4}×5×0.02+4×1{0}^{-6}×10}{4×1{0}^{-4}}$=0.15N/C;
(2)滑块从A到O点的过程,根据动能定理有E1qSAO-mgSAO-Wf=$\frac{1}{2}$m${v}_{0}^{2}$-0;
代入数据得:Wf=1×10-5J;
(3)电场力:E2q=3×10-5N,
重力:mg=4×10-5N,
根据平行四边形定则:F合=5×10-5N,tanθ=$\frac{3}{4}$,即合力与y轴负方向的夹角为37°;
将v0分解为垂直于合力和沿合力的分速度,垂直合力方向的分速度v01=3m/s,沿合力方向的分速度v02=4m/s;
加速度a=$\frac{{F}_{合}}{m}$=12.5m/s2;
当沿合力方向速度减为0时,速度最小vmin=v01=3m/s;
答:(1)求电场强度的大小E1为0.15N/C;
(2)小滑块从A点开始运动到原点O的过程中克服摩擦力做的功.
(3)小滑块从管口射出后的最小速度为3m/s.
点评 本题考查综合运用牛顿定律、动能定理、运动学公式等知识的能力.解答本题的关键是对滑块的运动过程进行分段分析,分析每段中的受力情况和运动情况,必要时做出小球的运动轨迹,再进行细心的计算.解答本题要求要有较强的物理问题分析能力和较强的计算力.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 根据公式v=$\sqrt{\frac{GM}{r}}$,可知卫星运动的线速度将减小到$\frac{v}{\sqrt{2}}$ | |
| B. | 根据公式F=m$\frac{{v}^{2}}{r}$,可知卫星所需的向心力将减小到原来的$\frac{1}{2}$ | |
| C. | 根据公式ω=$\frac{v}{r}$,可知卫星的角速度将减小到$\frac{ω}{2}$ | |
| D. | 根据F=G$\frac{Mm}{{r}^{2}}$,可知卫星的向心力减小为原来的$\frac{1}{4}$ |

| A. | 物体在0~8s时间内的位移方向沿x轴负方向 | |
| B. | 物体在0~2s时间内做匀减速运动 | |
| C. | 物体在2s~4s时间内发生的位移是12m | |
| D. | 物体在t=1s时刻的速度大于t=6s时刻的速度 |

| A. | 到达底端时两球的动能相等 | B. | 到达底端时两球重力的功率相等 | ||
| C. | 下滑过程两球重力所做的功不等 | D. | 下滑不同高度时两球的机械能相等 |
 如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°(sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6),以最低点C所在的水平面为重力势能的参考平面,则( )
如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°(sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6),以最低点C所在的水平面为重力势能的参考平面,则( )| A. | A、B两球所受弹力的大小之比为4:3 | B. | A、B两球运动的周期之比为1:1 | ||
| C. | A、B两球的动能之比为64:27 | D. | A、B两球的重力势能之比为16:9 |
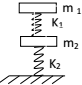 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )| A. | $\frac{{m}_{1}g}{{k}_{1}}$ | B. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{2}g}{{k}_{2}}$ | C. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{1}g}{{k}_{2}}$ | D. | $\frac{{(m}_{1}{+m}_{2})g}{{k}_{1}}$ |
| A. | 相互作用的物体,如果所受合外力为零,则它们的总动量保持不变 | |
| B. | 动量守恒是相互作用的物体系统在相互作用过程中的任何时刻动量之和都是一样的 | |
| C. | 动量守恒是相互作用的各个物体组成的系统在相互作用前的动量之和与相互作用之后的动量之和是一样的 | |
| D. | 动量守恒是指相互作用的各个物体在相互作用前后的动量不变 |
 一个质量为m的小铁块沿半径为R的固定半圆轨道上边缘由静止滑下,到半圆底部,问:
一个质量为m的小铁块沿半径为R的固定半圆轨道上边缘由静止滑下,到半圆底部,问: 如图所示,由运载火箭将飞船送入近地点为A、远地点为B的椭圆轨道上,A点距地面的高度为h1,飞船飞行五圈后进行变轨,进入预定圆轨道在预定圆轨道上飞行N圈所用时间为t.已知地球表面重力加速度为g,地球半径为R.求:
如图所示,由运载火箭将飞船送入近地点为A、远地点为B的椭圆轨道上,A点距地面的高度为h1,飞船飞行五圈后进行变轨,进入预定圆轨道在预定圆轨道上飞行N圈所用时间为t.已知地球表面重力加速度为g,地球半径为R.求: