题目内容
12. 如图所示,由运载火箭将飞船送入近地点为A、远地点为B的椭圆轨道上,A点距地面的高度为h1,飞船飞行五圈后进行变轨,进入预定圆轨道在预定圆轨道上飞行N圈所用时间为t.已知地球表面重力加速度为g,地球半径为R.求:
如图所示,由运载火箭将飞船送入近地点为A、远地点为B的椭圆轨道上,A点距地面的高度为h1,飞船飞行五圈后进行变轨,进入预定圆轨道在预定圆轨道上飞行N圈所用时间为t.已知地球表面重力加速度为g,地球半径为R.求:(1)飞船在A点的加速度大小aA;
(2)远地点B距地面的高度h2;
(3)沿着椭圆轨道从A到B的时间tAB.
分析 (1)由黄金代换确定出地球质量.飞船在A点由万有引力产生加速度求得加速度.
(2)根据万有引力提供向心力用周期关系即可求解高度;
(3)根据开普勒第三定律,结合椭圆轨道半长轴的大小,求出飞船在椭圆轨道上的周期,从而求出飞船由A点到B点所需的时间.
解答 解:(1)地表:GM=gR2 ①
在A点:a=$\frac{GM}{{r}^{2}}$=$\frac{GM}{(R+{h}_{1})^{2}}$ ②
由①②式可得:a=$g\frac{{R}^{2}}{(R+{h}_{1})^{2}}$
(2)在B点:$G\frac{M}{(R+{h}_{2})^{2}}=m(R+{h}_{2})\frac{4{π}^{2}}{{T}^{2}}$ ③
由①③式可得:${h}_{2}=\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R 而T=$\frac{t}{N}$,则h2=$\root{3}{\frac{g{R}^{2}{t}^{2}}{4{π}^{2}{N}^{2}}}-R$
(3)根据题意得椭圆轨道的半长轴r=$\frac{2R+{h}_{1}+{h}_{2}}{2}$=$\frac{\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}+R+{h}_{1}}{2}$,设椭圆周期为T′
根据开普勒第三定律得:$\frac{{r}^{3}}{T{′}^{2}}=\frac{(R+{h}_{2})^{3}}{(\frac{t}{N})^{2}}$ 得T′=$\sqrt{\frac{(\frac{t}{N})^{2}{r}^{3}}{(R+{h}_{2})^{3}}}$=$\sqrt{\frac{({\frac{t}{N})}^{2}(\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}+R+{h}_{1})^{3}}{(R+{h}_{2})^{3}}}$
则由A到B历时为$\frac{T′}{2}$=$\frac{1}{2}$$\sqrt{\frac{({\frac{t}{N})}^{2}(\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}+R+{h}_{1})^{3}}{(R+{h}_{2})^{3}}}$
答:(1)飞船在A点的加速度大小为$g\frac{{R}^{2}}{(R+{h}_{1})^{2}}$
(2)远地点B距地面的高度为$\root{3}{\frac{g{R}^{2}{t}^{2}}{4{π}^{2}{N}^{2}}}-R$
(3)沿着椭圆轨道从A到B的时间为$\frac{1}{2}$$\sqrt{\frac{({\frac{t}{N})}^{2}(\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}+R+{h}_{1})^{3}}{(R+{h}_{2})^{3}}}$
点评 本题主要考查了万有引力提供向心力公式的直接应用,注意选取适当的公式解题,难度适中;飞船由A点到B点所需的时间应是椭圆轨道的半个周期.关键掌握开普勒第三定律,并能灵活运用.

| A. | 砸钉子时不用橡皮锤,只是因为橡皮锤太轻 | |
| B. | 跳远时在沙坑里填沙,是为了减小冲量 | |
| C. | 在推车时推不动是因为推力的冲量为零 | |
| D. | 船舷常常悬挂旧轮胎,是为了延长作用时间,减小作用力 |
 如图所示为氢原子能级示意图的一部分,一群原来处于n=4能级的氢原子跃迁到n=1能级的过程中( )
如图所示为氢原子能级示意图的一部分,一群原来处于n=4能级的氢原子跃迁到n=1能级的过程中( )| A. | 放出三种频率不同的光子 | |
| B. | 放出六种频率不同的光子 | |
| C. | 氢原子放出光子后,核外电子运动的动能将减小 | |
| D. | 从n=4的能级跃迁到n=3的能级时,辐射出的光子的波长最短 |
 如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,用这些光子照射逸出功为2.49eV的金属钠,下列说法中正确的是( )
如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,用这些光子照射逸出功为2.49eV的金属钠,下列说法中正确的是( )| A. | 这群氢原子能辐射出三种频率不同的光,其中从n=3跃迁到n=2所发出的光波长最短 | |
| B. | 这群氢原子在辐射光子的过程中电子绕核运动的动能减小 | |
| C. | 金属钠表面所发出的光电子的最大初动能为11.11 eV | |
| D. | 金属钠表面所发出的光电子的最大初动能为9.60 eV |
 如图所示,小球a、b的质量分别是m和2m,a从倾角为30°的光滑固定斜面的顶端无初速下滑,b从斜面等高处以初速度v0平抛,比较a、b落地的运动过程有( )
如图所示,小球a、b的质量分别是m和2m,a从倾角为30°的光滑固定斜面的顶端无初速下滑,b从斜面等高处以初速度v0平抛,比较a、b落地的运动过程有( )| A. | 所用的时间相同 | B. | a、b都做匀变速运动 | ||
| C. | 落地前的速度相同 | D. | a、b所受合力相同 |
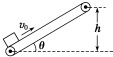 如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行,现把一质量为m=10kg的工件(可看做质点)轻轻放在传送带的底端,工件与传送带之间的摩擦系数μ=$\frac{\sqrt{3}}{2}$,经过时间t=1.9s,工件被传送到顶端,取g=10m/s2求:
如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行,现把一质量为m=10kg的工件(可看做质点)轻轻放在传送带的底端,工件与传送带之间的摩擦系数μ=$\frac{\sqrt{3}}{2}$,经过时间t=1.9s,工件被传送到顶端,取g=10m/s2求: