题目内容
6. 一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状.此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面.如图所示,以沟底的O点为原点建立坐标系Oxy.已知,山沟竖直一侧的高度为h,坡面的抛物线方程为y=$\frac{1}{h}{x^2}$,探险队员的质量为m.人视为质点,忽略空气阻力,重力加速度为g.
一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状.此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面.如图所示,以沟底的O点为原点建立坐标系Oxy.已知,山沟竖直一侧的高度为h,坡面的抛物线方程为y=$\frac{1}{h}{x^2}$,探险队员的质量为m.人视为质点,忽略空气阻力,重力加速度为g.(1)求此人落到坡面试的动能;
(2)此人水平跳出的速度为多大时,他落在坡面时的动能最小?动能的最小值为多少?
分析 (1)由平抛运动规律列出等式.由整个过程中根据由动能定理求解即可
(2)根据动能的表达式应用数学方法求解.
解答 解:(1)设探险队员跳到坡面上时水平位移为x,竖直位移为H,
由平抛运动规律有:x=v0t,H=$\frac{1}{2}$gt2,
整个过程中,由动能定理可得:mgH=EK-$\frac{1}{2}$mv02
由几何关系,y=2h-H
坡面的抛物线方程y=$\frac{1}{2h}$x2
解以上各式得:EK=$\frac{1}{2}$mv02+$\frac{4m{g}^{2}{h}^{2}}{{v}_{0}^{2}+gh}$
(2)将EK=$\frac{1}{2}$mv02+$\frac{4m{g}^{2}{h}^{2}}{{v}_{0}^{2}+gh}$改写为
${E_k}=\frac{1}{4}m(2v_0^2+gh)+\frac{{m{g^2}{h^2}}}{2v_0^2+gh}-\frac{1}{4}mgh$
$当\frac{1}{4}m(2v_0^2+gh)=\frac{{m{g^2}{h^2}}}{2v_0^2+gh}时$
$即v_0^{\;}=\sqrt{\frac{1}{2}gh}时$,
${E_{kmin}}=\frac{3}{4}mgh$
答:(1)此人落到坡面时的动能是:$\frac{1}{2}$mv02+$\frac{4m{g}^{2}{h}^{2}}{{v}_{0}^{2}+gh}$
(2)此人水平跳出的速度为$\sqrt{\frac{gh}{2}}$时,他落在坡面时的动能最小,动能的最小值为$\frac{3mgh}{4}$
点评 本题主要考查平抛运动和动能定理的应用,以及函数最值的计算,意在考查考生的综合分析及数学计算能力.对学生应用数学规律解物理问题的能力要求较高.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案 如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )
如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )| A. | 此时两臂受到的压力大小均为5.0×104N | |
| B. | 此时千斤顶对汽车的支持力为2.0×105N | |
| C. | 若继续摇动把手,将汽车顶起,两臂受到的压力将增大 | |
| D. | 若继续摇动把手,将汽车顶起,两臂受到的压力将减小 |
 如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,有两个可视为质点且质量相同的小球A和B,在球面内壁两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为a=53°和β=37°,则(sin37°=0.6)( )
如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,有两个可视为质点且质量相同的小球A和B,在球面内壁两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为a=53°和β=37°,则(sin37°=0.6)( )| A. | A、B两球所受支持力的大小之比为3:4 | |
| B. | A、B两球运动的周期之比为2:$\sqrt{3}$ | |
| C. | A、B两球的角速度之比为2:$\sqrt{3}$ | |
| D. | A、B两球的线速度之比为8:3$\sqrt{3}$ |
| A. | $\frac{x_1}{{{t_1}^2}}=\frac{x_2}{{{t_2}^2}}=\frac{x_3}{{{t_3}^2}}$ | B. | $\frac{x_1}{t_1}<\frac{x_2}{t_2}<\frac{x_3}{t_3}$ | ||
| C. | $\frac{x_1}{t_1}=\frac{x_2}{t_2}=\frac{x_3}{t_3}$ | D. | $\frac{x_1}{{{t_1}^2}}<\frac{x_2}{{{t_2}^2}}<\frac{x_3}{{{t_3}^2}}$ |
 如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙(速度恒定不变),甲的速度为v0.物体离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0.物体与乙之间的动摩擦因数为μ.重力加速度为 g.若乙的宽度足够大,下列说法正确的( )
如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙(速度恒定不变),甲的速度为v0.物体离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0.物体与乙之间的动摩擦因数为μ.重力加速度为 g.若乙的宽度足够大,下列说法正确的( )| A. | 物体刚滑上乙传送带时,受到摩擦力大小为μmg | |
| B. | 物体刚滑上乙传送带时,受到摩擦力大小为$\sqrt{2}$μmg | |
| C. | 物体在乙上侧向( 垂直于乙的运动方向) 滑过的距离为$\frac{\sqrt{2}{{v}_{0}}^{2}}{2μg}$ | |
| D. | 物体在乙上侧向( 垂直于乙的运动方向) 滑过的距离为$\frac{\sqrt{2}{{v}_{0}}^{2}}{μg}$ |
 请完成下列判断(判断语句如下:“不变”、“增大”或“减少”,“有”或“无”,或判断方向:从左向右或从右向左等),并将正确答案直接填写在横线上或空格处:
请完成下列判断(判断语句如下:“不变”、“增大”或“减少”,“有”或“无”,或判断方向:从左向右或从右向左等),并将正确答案直接填写在横线上或空格处:
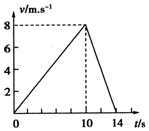 一物体由静止开始运动的速度-时间关系图象如图,求:
一物体由静止开始运动的速度-时间关系图象如图,求: