题目内容
14. 如图所示,匀强磁场B=0.1T,所用矩形线圈的匝数N=100,边长ab=0.2m,bc=0.5m,以角速度ω=100π rad/s绕OO′轴匀速转动,线圈电阻为22Ω.从线圈平面通过中性面时开始计时,试求:
如图所示,匀强磁场B=0.1T,所用矩形线圈的匝数N=100,边长ab=0.2m,bc=0.5m,以角速度ω=100π rad/s绕OO′轴匀速转动,线圈电阻为22Ω.从线圈平面通过中性面时开始计时,试求:(1)线圈中感应电动势的瞬时值;
(2)线圈电流的有效值.
分析 (1)线圈中产生的感应电动势的最大值表达式为Em=NBSω,写出感应电动势的瞬时表达式
(2)根据E=$\frac{{E}_{m}}{\sqrt{2}}$和欧姆定律求出电流的有效值.
解答 解:感应电动势的瞬时值e=NBSωsinωt,由题可知S═0.2×0.5 m2=0.1 m2,
Em=NBSω=100×0.1×0.1×100π V=314 V,
所以e=314sin 100πt V.
(2)线圈电流的有效值$I=\frac{NBSω}{\sqrt{2}R}=10A$
答:(1)线圈中感应电动势的瞬时值为e=314sin 100πt V;
(2)线圈电流的有效值为10A.
点评 解决本题的关键知道正弦式交流电峰值的表达式Em=nBSω,能够结合图象求出电动势的瞬时表达式.

练习册系列答案
相关题目
2.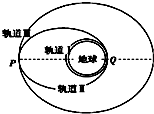 在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )
在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )
 在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )
在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )| A. | 卫星在轨道Ⅲ上运行的加速度为($\frac{h}{R+h}$)2g | |
| B. | 卫星在轨道Ⅲ上运行的线速度为v=$\sqrt{\frac{g{R}^{2}}{R+h}}$ | |
| C. | 卫星在轨道Ⅲ上运行时经过P点的速率等于在轨道Ⅱ上运行时经过P点的速率 | |
| D. | 卫星在轨道Ⅲ上的机械能小于在轨道Ⅰ上的机械能 |
9.关于图甲、乙、丙、丁,下列说法正确的是( )


| A. | 图甲中电流的峰值为2A,有效值为2.5$\sqrt{2}$ A,周期为5s | |
| B. | 图乙中电流的峰值为5A,有效值为2.5A | |
| C. | 图丙中电流的峰值为2A,有效值为 1A | |
| D. | 图丁中电流的最大值为4A,有效值为 $\sqrt{13.5}$A,周期为2s |
6. 如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )
如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )
 如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )
如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )| A. | a与圆盘间的静摩擦力先达到最大值 | |
| B. | 当ω>$\sqrt{\frac{μg}{2l}}$时,绳上出现张力 | |
| C. | 当a、b与圆盘间静摩擦力都达到最大值时,绳上张力为3μmg | |
| D. | 转速太大时,b将远离圆心运动 |
3.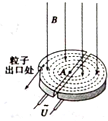 1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )
1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )
 1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )
1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )| A. | 粒子被加速后的最大速度不可能超过2πRf | |
| B. | 粒子离开回旋加速器时的最大动能与加速电压U成正比 | |
| C. | 粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比为$\sqrt{2}$:1 | |
| D. | 若考虑相对论效应,速率接近光速时粒子的质量会随速率有显著增加 |
4. 如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )
如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )
 如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )
如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )| A. | 小球经过B点时,小球的动能为mgL | |
| B. | 小球经过B点时,绳子的拉力为3mg | |
| C. | 小球下摆过程中,重力对小球做功的平均功率为0 | |
| D. | 小球下摆过程中,重力对小球做功的瞬时功率先增大后减小 |
 如图所示,两端封闭的玻璃管中间有一段长为h=16cm的水银柱,在27℃的室内水平放置,水银柱把玻璃管中的气体分成长度都是L0=40cm的A、B两部分,两部分气体的压强均为p0=30cmHg.现将A端抬起使玻璃管竖直
如图所示,两端封闭的玻璃管中间有一段长为h=16cm的水银柱,在27℃的室内水平放置,水银柱把玻璃管中的气体分成长度都是L0=40cm的A、B两部分,两部分气体的压强均为p0=30cmHg.现将A端抬起使玻璃管竖直
 某交流发电机产生的感应电动势与时间的关系如图所示,该发电机线圈的内阻为r=2Ω.
某交流发电机产生的感应电动势与时间的关系如图所示,该发电机线圈的内阻为r=2Ω.