题目内容
17. 如图在一足够大的真空玻璃罩中,光滑半圆形轨道竖直固定在光滑水平板面上(图中阴影部分),轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落在板面上的点距M点的水平距离为2R,重力加速度为g,忽略圆管内径,求:
如图在一足够大的真空玻璃罩中,光滑半圆形轨道竖直固定在光滑水平板面上(图中阴影部分),轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落在板面上的点距M点的水平距离为2R,重力加速度为g,忽略圆管内径,求:(1)粘合后的两球从飞出轨道到落到板面上的时间t;
(2)小球A冲进轨道时速度v的大小.
分析 (1)粘合后的两球从飞出轨道后做平抛运动,而平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出平抛运动的时间.
(2)根据落地的水平位移求出结合体的初速度,根据动量守恒定律求出A球与B球碰撞前的速度,再根据机械能守恒定律求出小球A冲进轨道时速度v的大小.
解答 解 (1)粘合后的小球A和小球B,飞出轨道后做平抛运动,竖直方向分运动为自由落体运动,有:
2R=$\frac{1}{2}g{t}^{2}$-----------------①
解得:t=2$\sqrt{\frac{R}{g}}$------------------------②
(2)设球A的质量为m,碰撞前速度大小为v1,把求A冲进轨道最点处的重力势能定为0,由机械能守恒定律知:
$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}m{v}_{1}^{2}$+2mgR--------------③
设碰撞后粘在一起的两球的速度为v2,取向左为正方向,由动量守恒定律知:
mv1=2mv2-----------------------④
飞出轨道后做平抛运动,水平方向分运动为匀速直线运动,有
2R=v2t----------------------------⑤
联立②③④⑤几式可得:v=2$\sqrt{2gR}$-----------------⑥
答:(1)粘合后的两球从飞出轨道到落到板面上的时间t是2$\sqrt{\frac{R}{g}}$;
(2)小球A冲进轨道时速度v的大小是2$\sqrt{2gR}$.
点评 本题综合考查了动量守恒定律、机械能守恒定律和平抛运动的规律,关键是理清物理过程,选择合适的规律进行求解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
7.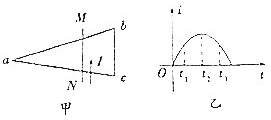 等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
 等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )| A. | 在任何时刻线框中都无感应电流 | |
| B. | 在t1时刻线框中有沿acba方向的感应电流 | |
| C. | 在t2时刻线框中有沿acba方向的感应电流 | |
| D. | 在t3时刻线框中有沿abca方向的感应电流 |
8. 如图所示,物体A和B质量均为m,且分别与轻绳连结跨过光滑轻质定滑轮,当用力F拉B沿水平面向右匀速运动过程中,绳对A的拉力的大小是( )
如图所示,物体A和B质量均为m,且分别与轻绳连结跨过光滑轻质定滑轮,当用力F拉B沿水平面向右匀速运动过程中,绳对A的拉力的大小是( )
 如图所示,物体A和B质量均为m,且分别与轻绳连结跨过光滑轻质定滑轮,当用力F拉B沿水平面向右匀速运动过程中,绳对A的拉力的大小是( )
如图所示,物体A和B质量均为m,且分别与轻绳连结跨过光滑轻质定滑轮,当用力F拉B沿水平面向右匀速运动过程中,绳对A的拉力的大小是( )| A. | 大于mg | B. | 等于F | C. | 总等于mg | D. | 小于mg |
5. 如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )
如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )
 如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )
如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )| A. | 小球在tB时刻所受弹簧弹力等于0.5mg | |
| B. | 整个过程小球的机械能守恒 | |
| C. | 小球从tC时刻所在的位置由静止释放后,不能回到出发点 | |
| D. | 小球从tA时刻到tC时刻的过程中重力势能的减少量小于弹簧弹性势能的增加量 |
9.如图甲所示,一质量为m的物块在t=0时刻,以初速度v0从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示.t0时刻物块到达最高点,3t0时刻物块又返回底端.下列说法正确的是( )


| A. | 物块从开始运动到返回底端的过程中重力的冲量大小为2mgt0 | |
| B. | 物块从t=0时刻开始运动到返回底端的过程中动量的变化量为-$\frac{3}{2}$mv0 | |
| C. | 斜面倾角θ的正弦值为$\frac{5{v}_{0}}{8g{t}_{0}}$ | |
| D. | 不能求出3t0时间内物块克服摩擦力所做的功 |
7.分子动理论较好地解释了物质的宏观热力学性质.据此可判断下列说法中正确的是( )
| A. | 显微镜下观察到墨水中的小炭粒在不停的做无规则运动,这反映了液体分子运动的无规则性 | |
| B. | 分子势能随着分子间距离的增大,总是先减小后增大 | |
| C. | 当分子间的引力大于斥力时,宏观物体呈现固态;当分子间的引力小于斥力时,宏观物体呈现气态 | |
| D. | 分子间的相互作用力随着分子间距离的增大,一定先减小后增大 | |
| E. | 在真空、高温条件下,可以利用分子扩散向半导体材料掺入其它元素 |
 如图1所示,在“利用自由落体运动验证机械能守恒定律”的实验中,让重锤拖着穿过打点计时器的纸带做自由落体运动,测量重锤的重力势能减少量和动能增加量,从而验证机械能守恒定律.
如图1所示,在“利用自由落体运动验证机械能守恒定律”的实验中,让重锤拖着穿过打点计时器的纸带做自由落体运动,测量重锤的重力势能减少量和动能增加量,从而验证机械能守恒定律.


