题目内容
19. 如图所示的直角坐标系中,在直线x=-2a到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴正方向,x轴下方的电场方向沿y轴负方向.一群电荷量为-q、质量为m的粒子被加速电压U0加速后,从电场左边界上A(-2a,a)到C(-2a,0)区域内,依次连续沿x轴正方向射入有界匀强电场.从A点射入的粒子,恰好从y轴上的A′(0,-a)沿x轴正方向射出有界匀强电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用
如图所示的直角坐标系中,在直线x=-2a到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴正方向,x轴下方的电场方向沿y轴负方向.一群电荷量为-q、质量为m的粒子被加速电压U0加速后,从电场左边界上A(-2a,a)到C(-2a,0)区域内,依次连续沿x轴正方向射入有界匀强电场.从A点射入的粒子,恰好从y轴上的A′(0,-a)沿x轴正方向射出有界匀强电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用(1)求匀强电场的电场强度E的大小.
(2)粒子在AC间的位置坐标y为何值时,粒子通过电场后速度沿x轴正方向?
(3)若以直线x=2a上的某点为圆心的圆形区域内,存在垂直xOy平面向里的匀强磁场,使沿x轴正方向射出电场的粒子,经磁场偏转后,都能通过直线x=2a与圆形磁场边界的一个交点处而被收集,求圆形磁场区域的最小面积Smin及相应磁感应强度B的大小.
分析 (1)根据动能定理求加速后粒子的速度.粒子进入上方的匀强电场中做的是类平抛运动,水平方向上是匀速运动,由匀速运动的规律可以求得粒子的运动的时间;
竖直方向作匀加速直线运动,根据位移公式和对称性列式求解.
(2)粒子通过电场后速度沿x轴正方向必须满足:2a=n•2△x,△x是粒子第一次到达x轴时水平位移,再结合类平抛运动的分位移规律求解.
(3)根据上题的结论讨论分析粒子沿x轴正方向射出的坐标,由几何知识分析和求解圆形磁场区域的最小面积Smin.根据匀速圆周运动的规律可以求得磁感应强度的大小.
解答 解:(1)设粒子加速后速度大小为v0,据动能定理有 qU0=$\frac{1}{2}m{v}_{0}^{2}$
设粒子由A运动到A′的时间为t,据类平抛运动的规律和对称性得:
x方向有 2a=v0t
y方向有 2a=2×$\frac{1}{2}•$$\frac{qE}{m}(\frac{t}{2})^{2}$
解得 E=$\frac{4{U}_{0}}{a}$
(2)设满足条件的粒子到C点的距离为△y,粒子第一次到达x轴的时间为△t,水平位移为△x,则有
△x=v0△t
△y=$\frac{1}{2}•\frac{qE}{m}(△t)^{2}$
当满足 2a=n•2△x时,粒子从电场射出时速度方向必沿x轴正方向
解得△y=$\frac{1}{{n}^{2}}$•$\frac{1}{2}•\frac{qE}{m}•(\frac{a}{{v}_{0}})^{2}$=$\frac{a}{{n}^{2}}$
则 y=$\frac{a}{{n}^{2}}$(n=1,2,3,…)
(3)如图所示,当n=1时,粒子沿x轴正方向射出的坐标为 y1=-a.
当n=2时,粒子沿x轴正方向射出的坐标为 y2=$\frac{a}{4}$.
当n≥3时,沿x轴正方向射出的粒子必分布在y1到y2之间,y1到y2之间的距离 L=y2-y1=$\frac{5}{4}$a
故磁场的最小半径 Rmin=$\frac{L}{2}$=$\frac{5}{8}$a
磁场的最小面积为 Smin=$π{R}_{min}^{2}$=$\frac{25π{a}^{2}}{64}$
如图所示,欲使粒子磁场偏转后汇聚于一点,粒子运动半径与磁场圆半径应相等,图中轨迹圆与磁场圆相交,四边形PO1QO2为菱形.
据洛伦兹力提供向心力,有qv0B=m$\frac{{v}_{0}^{2}}{R}$
解得 B=$\frac{8}{5a}\sqrt{\frac{2m{U}_{0}}{q}}$
答:
(1)匀强电场的电场强度E的大小为$\frac{4{U}_{0}}{a}$.
(2)粒子在AC间的位置坐标y=$\frac{a}{{n}^{2}}$(n=1,2,3,…)时,粒子通过电场后速度沿x轴正方向.
(3)形磁场区域的最小面积Smin是$\frac{25π{a}^{2}}{64}$,相应磁感应强度B的大小为$\frac{8}{5a}\sqrt{\frac{2m{U}_{0}}{q}}$.
点评 本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
| A. | 0~x1范围内各点场强的方向均与x轴平行 | |
| B. | 只在电场力作用下,正电荷沿x轴从0运动到x1,可做匀减速直线运动 | |
| C. | 负电荷沿x轴从x2移到x3的过程中,电场力做正功,电势能减小 | |
| D. | 无法比较x2~x3与x4~x5间的场强大小 |
 如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自耦变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )
如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自耦变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )| A. | 此时原副线圈的匝数比为2:1 | |
| B. | 此时电流表的示数为0.4A | |
| C. | 若将自耦变压器触头向下滑动,灯泡会变亮 | |
| D. | 若将滑动变阻器滑片向上移动,则电流表示数增大 |
 如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )
如图所示,一横截面为等腰三角形的玻璃三棱镜,其顶角θ为锐角,折射率为2.现在横截面内有一光线从其左侧而上半部分射入棱镜,不考虑棱镜内部的反射.若保持入射光线在过入射点的法线的下方一侧,且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角目的取值范围是( )| A. | 0°<θ<30° | B. | 0°≤θ≤30° | C. | 30°≤θ<45° | D. | 30°≤θ<60° |
 一个圆沿一直线无滑动地滚动,则圆上一固定点所经过的轨迹称为摆线.在竖直平面内有xOy坐标系,空间存在垂直xOy平面向里的匀强磁场,磁感应强度为B,一质量为m、电荷量为+q的小球从坐标原点由静止释放,小球的轨迹就是摆线.小球在O点速度为0时,可以分解为大小始终相等的一水平向右和一水平向左的两个分速度,如果速度大小取适当的值,就可以把小球的运动分解成以v0的速度向右做匀速直线运动和从O点以v1为初速度做匀速圆周运动两个分运动.设重力加速度为g,下列式子正确的是( )
一个圆沿一直线无滑动地滚动,则圆上一固定点所经过的轨迹称为摆线.在竖直平面内有xOy坐标系,空间存在垂直xOy平面向里的匀强磁场,磁感应强度为B,一质量为m、电荷量为+q的小球从坐标原点由静止释放,小球的轨迹就是摆线.小球在O点速度为0时,可以分解为大小始终相等的一水平向右和一水平向左的两个分速度,如果速度大小取适当的值,就可以把小球的运动分解成以v0的速度向右做匀速直线运动和从O点以v1为初速度做匀速圆周运动两个分运动.设重力加速度为g,下列式子正确的是( )| A. | 速度v0所取的适当值应为$\frac{mg}{2qB}$ | |
| B. | 经过t=$\frac{2πm}{qB}$第一次到达摆线最低点 | |
| C. | 最低点的y轴坐标为y=$\frac{-{m}^{2}g}{{q}^{2}{B}^{2}}$ | |
| D. | 最低点的速度为2v0 |
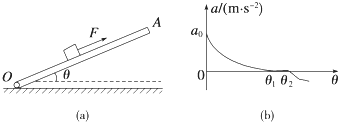
| A. | 由图象可知木板与水平面的夹角处于θ1和θ2之间时,物块所受摩擦力一定为零 | |
| B. | 由图象可知木板与水平面的夹角大于θ2时,物块所受摩擦力不一定沿木板向上 | |
| C. | 根据题意可以计算得出物块加速度a0的大小为6m/s2 | |
| D. | 根据题意可以计算当θ=45°时,物块所受摩擦力为Ff=μmgcos 45°=$\sqrt{2}$N |
 如图所示,在xOy平面内,以O1(-R,0)为圆心,R为半径的圆内有垂直于xOy平面向里的匀强磁场,在y轴的右侧等腰三角形OAB区域内,存在一方向垂直于xOy平面向外的匀强磁场,其右边界AB与y轴平行,∠AOB=120°,边界AB与X轴相交于C点,两区域磁感应强度大小相等.在圆心磁场的上册-2R<x<0的区间内有一粒子发射器,该发射器中在平行于x轴的方向上均匀分布着一簇带电粒子,其质量为m、电荷量为q(q>0),这写粒子在控制其的控制下能以v0的速度同时沿y轴负方向射入圆形磁场区域.在第二象限内x<-2R的某一区域内存在一个水平加速电场,该电场的电压为U,一质量也为m、电荷量也为q(q>0)的S粒子,在该电场中由静止加速后以某一速度打到控制器的触发器上(图中未画出),控制器就发射粒子,这些粒子经圆形磁场区域偏转后都从0点进入y轴右侧,部分粒子进入OAB区域内.不计粒子重力和粒子间的相互作用.求:
如图所示,在xOy平面内,以O1(-R,0)为圆心,R为半径的圆内有垂直于xOy平面向里的匀强磁场,在y轴的右侧等腰三角形OAB区域内,存在一方向垂直于xOy平面向外的匀强磁场,其右边界AB与y轴平行,∠AOB=120°,边界AB与X轴相交于C点,两区域磁感应强度大小相等.在圆心磁场的上册-2R<x<0的区间内有一粒子发射器,该发射器中在平行于x轴的方向上均匀分布着一簇带电粒子,其质量为m、电荷量为q(q>0),这写粒子在控制其的控制下能以v0的速度同时沿y轴负方向射入圆形磁场区域.在第二象限内x<-2R的某一区域内存在一个水平加速电场,该电场的电压为U,一质量也为m、电荷量也为q(q>0)的S粒子,在该电场中由静止加速后以某一速度打到控制器的触发器上(图中未画出),控制器就发射粒子,这些粒子经圆形磁场区域偏转后都从0点进入y轴右侧,部分粒子进入OAB区域内.不计粒子重力和粒子间的相互作用.求: 如图所示,半径为R的绝缘光滑圆环固定在竖直平面内,环上套一质量为m且带正电荷的珠子,空间存在水平向右的匀强电场,珠子所受静电力是其重力的$\frac{3}{4}$倍,将珠子从环上最低位置A点静止释放.
如图所示,半径为R的绝缘光滑圆环固定在竖直平面内,环上套一质量为m且带正电荷的珠子,空间存在水平向右的匀强电场,珠子所受静电力是其重力的$\frac{3}{4}$倍,将珠子从环上最低位置A点静止释放.