题目内容
2.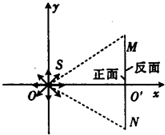 如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的带正电的粒子,位于y轴的右侧有一垂直于z轴、长度为L的很薄的荧光屏MN,荧光屏正反面两侧均涂有荧光粉,MN与x轴交于点O′.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,电荷量为q,速度大小为v,不计粒子的重力.
如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的带正电的粒子,位于y轴的右侧有一垂直于z轴、长度为L的很薄的荧光屏MN,荧光屏正反面两侧均涂有荧光粉,MN与x轴交于点O′.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,电荷量为q,速度大小为v,不计粒子的重力.(1)若只在y轴右侧加一平行于x轴正方向的匀强电场,要使y轴右侧射出的所有粒子都能打到荧光屏MN上,试求电场强度的最小值Emin及打到荧光屏M点时粒子的动能.
(2)若在xOy平面内只加一方向垂直纸面向里的匀强磁场,要使粒子能打到荧光屏MN的反面O′点上,试求磁场的磁感应强度的最大值Bmax.
(3)若在xOy平面内只加一方向垂直纸面向里的匀强磁场,磁感应强度与(2)中所求Bmax相同,试求粒子打到荧光屏MN正面O′点所需的时间t1和打在荧光屏MN反面O′点所需的时间t2之比.
分析 (1)要使y轴右侧射出的所有粒子都能打到荧光屏MN上,临界状态为对应沿着y轴正方向射出的带电粒子正好打在荧光屏的端点M,根据类平抛运动的规律,求出电场强度的最小值,根据动能定理求出粒子打到荧光屏M点的动能.
(2)当磁感应强度最大时,轨道半径最小,作出粒子运动轨迹图,根据几何关系求出轨道半径的大小,从而根据洛伦兹力提供向心力求出磁感应强度的大小.
(3)作出粒子的运动轨迹图,分别求出打在正面O′点和反面O′点轨迹的圆心角,抓住圆周运动的角速度相等,求出运动时间之比.
解答 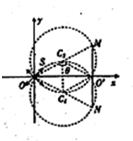 解:(1)由题意,所加电场电场强度的最小值为Emin,对应沿着y轴正方向射出的带电粒子正好打在荧光屏的端点M这一临界状态,对该粒子有:
解:(1)由题意,所加电场电场强度的最小值为Emin,对应沿着y轴正方向射出的带电粒子正好打在荧光屏的端点M这一临界状态,对该粒子有:
$\frac{L}{2}$=vt
$\frac{\sqrt{3}}{2}L$=$\frac{q{E}_{min}}{2m}{t}^{2}$
联立两式解得:Emin=$\frac{4\sqrt{3}m{v}^{2}}{qL}$
对此时从S射出能打到荧光屏上的任一粒子(包括打到荧光屏M点的粒子),设它到达屏时的动能为Ek,根据动能定理得:
Ek-$\frac{1}{2}m{v}^{2}$=qEmin•$\frac{\sqrt{3}}{2}$L
解得:Ek=$\frac{13}{2}$mv2.
(2)由题意得,所加磁场的最大磁感应强度Bmax对应来自S的粒子恰好经过荧光屏下端点N后打到O′这一临界状态,如图所示(圆心为C1)从图中的几何关系得,粒子在磁场中做圆周运动的半径为 r=$\frac{L}{2}$.
根据qvBmax=m$\frac{{v}^{2}}{r}$
解得:Bmax=$\frac{2mv}{qL}$.
(3)打在荧光屏正面O′点的粒子的圆弧如图(圆心在C2),根据匀速圆周运动规律有:
t1=$\frac{θ}{ω}$,
t2=$\frac{2π-θ}{ω}$
由图中几何关系得:θ=$\frac{2π}{3}$.
解得:t1:t2=1:2.
答:(1)电场强度的最小值Emin为$\frac{4\sqrt{3}m{v}^{2}}{qL}$,打到荧光屏M点的粒子的动能为$\frac{13}{2}$mv2.
(2)磁场的磁感应强度的最大值Bmax为$\frac{2mv}{qL}$.
(3)粒子打在-荧光屏MN的正面O'点所需的时问t1和打在荧光MN的反面O’点所需的时间t2之比为1:2.
点评 本题考查了粒子在电场中的类平抛运动,和在磁场中的圆周运动,综合性较强,关键作出临界的轨迹图,选择合适的规律进行求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 交流电表的示数 | B. | 灯泡的额定电压 | ||
| C. | 电容器的耐压值 | D. | 保险丝的额定电流 |
| A. | 2J | B. | 10J | C. | 12J | D. | 20J |
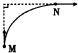 如图所示,一物体在水平恒力作用下沿光滑水平面做曲线运动,当物体从M点运动到N点时,其速度方向恰好改变了90°,则在此过程中,该物体的动能将( )
如图所示,一物体在水平恒力作用下沿光滑水平面做曲线运动,当物体从M点运动到N点时,其速度方向恰好改变了90°,则在此过程中,该物体的动能将( )| A. | 不断增大 | B. | 不断减小 | C. | 先减小后增大 | D. | 先增大后减小 |
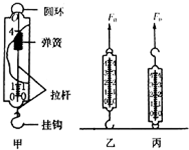 实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )| A. | 乙图读数F0-G,丙图读数F0+G | B. | 乙图读数F0+G,丙图读数F0-G | ||
| C. | 乙图读数F0,丙图读数F0-G | D. | 乙图读数F0-G,丙图读数F0 |
| A. | 是a=g的匀变速运动 | |
| B. | 可分解为竖直向上的匀速直线运动和自由落体运动 | |
| C. | 可以把从最高点下落的后半段运动看作是自由落体运动 | |
| D. | 上升过程的加速度小于下落过程的加速度 |
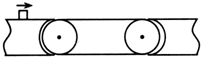 水平传送装置如图所示,一物块每次都以恒定的初速度由载物台冲上传送带,当传送带顺时针方向转动时,通过传送带所用时间为t1;当传送带逆时针方向转动时,通过传送带所用时间为t2;当传送带不动时,通过传送带所用时间为t3.下列判断正确的是( )
水平传送装置如图所示,一物块每次都以恒定的初速度由载物台冲上传送带,当传送带顺时针方向转动时,通过传送带所用时间为t1;当传送带逆时针方向转动时,通过传送带所用时间为t2;当传送带不动时,通过传送带所用时间为t3.下列判断正确的是( )| A. | 一定有t1<t2 | B. | 一定有t2>t3>t1 | C. | 可能有t1=t2=t3 | D. | 可能有t1<t2=t3 |
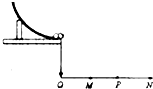 如图所示,在验证动量守恒的实验中:
如图所示,在验证动量守恒的实验中: