题目内容
10. 如图所示,一定质量的理想气体按p-T图象中箭头方向,从状态A变化到状态B,再变化到状态C,已知气体在状态A时的体积为33.6L.
如图所示,一定质量的理想气体按p-T图象中箭头方向,从状态A变化到状态B,再变化到状态C,已知气体在状态A时的体积为33.6L.(1)从状态A沿图中箭头变化到状态B的过程中,气体是吸热还是放热?简要说明理由.
(2)气体在状态C的体积是多少?
(3)已知阿伏加德罗常数为6.0×1023mol-1,在标准状况下,即压强p0=1.0×105Pa、温度为0℃时,任何气体的摩尔体积都为22.4L,问该气体的分子个数为多少?(结果取一位有效数字)
分析 (1)从A到B的过程中,气体的压强不变,温度升高,体积变大,根据热力学第一定律分析气体的内能的变化;
(2)A、C两个状态的温度相同,根据玻意耳定意可以求得体积的大小;
(3)根据理想气体状态方程先计算在标准状态下的体积,在计算分子的个数.
解答 解:(1)气体从状态A变化到状态B的过程为等压变化,由盖•吕萨克定律可知,气体温度升高,体积增大.由于气体在对外做功的同时内能增大,根据热力学第一定律知该过程吸热.
(2)A、C两个状态的温度相同,根据玻意耳定律得:pAVA=pCVC…①
解得:VC=67.2L…②
(3)根据理想气体状态方程得:$\frac{{{p_A}{V_A}}}{T_A}=\frac{{{p_0}{V_0}}}{T_0}$…③
其中T0=273K,所以气体的分子个数:$n=\frac{V_0}{{{V_{mol}}}}{N_A}$…④
解得:n=5×1024个…⑤
答:(1)吸热;
(2)气体在状态C的体积是67.2升;
(3)气体的分子个数5×1024个.
点评 以封闭的气体为研究对象,找出气体变化前后的状态参量,利用气体的状态方程计算即可.

练习册系列答案
相关题目
1. 一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )
一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )
 一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )
一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )| A. | $\frac{1}{3}$m/s | B. | 3m/s | C. | 15m/s | D. | 27m/s |
18.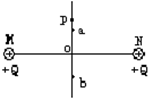 M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
 M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )| A. | 点电荷-q在a、b两点的速度一定相等 | |
| B. | 点电荷-q在a、b两点的动能一定相等 | |
| C. | 点电荷-q在a、b两点的加速度一定相等 | |
| D. | 点电荷-q做简谐运动 |
2.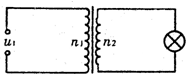 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )| A. | Um=200V | B. | Um=200$\sqrt{2}V$ | ||
| C. | 当ωt=$\frac{π}{2}$时,副线圈中的电流为O | D. | 当ωt=π时,副线圈中的电流为O |
 1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.在D盒中心A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.
1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.在D盒中心A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.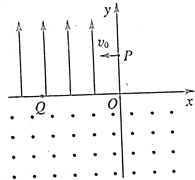 如图所示,在xOy平面内,第二象限中有匀强电场,方向沿y轴正方向,在第四象限有匀强磁场,方向垂直于xOy平面问外.今有一个质量为m,电量为e的电子(不计重力),从y轴上的P(0,L)点以垂直于y轴、大小为v0的初速度射入电场,经电场偏转后从x轴上的Q(-2L,0)点进入磁场,并能返回到出发点P.求:
如图所示,在xOy平面内,第二象限中有匀强电场,方向沿y轴正方向,在第四象限有匀强磁场,方向垂直于xOy平面问外.今有一个质量为m,电量为e的电子(不计重力),从y轴上的P(0,L)点以垂直于y轴、大小为v0的初速度射入电场,经电场偏转后从x轴上的Q(-2L,0)点进入磁场,并能返回到出发点P.求: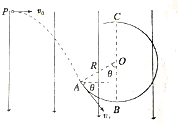 如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求:
如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求: 如图所示,质量为M=4kg,长为L=1.5m的长木板,静止在光滑水平面上.一质量为m=1kg的小木块放在木板的左端,小木块与木板间的动摩擦因数μ=0.4,取g=10m/s2.
如图所示,质量为M=4kg,长为L=1.5m的长木板,静止在光滑水平面上.一质量为m=1kg的小木块放在木板的左端,小木块与木板间的动摩擦因数μ=0.4,取g=10m/s2.