题目内容
11. 氢原子的能级如图所示,一群氢原子处于量子数n=4能极状态,则:
氢原子的能级如图所示,一群氢原子处于量子数n=4能极状态,则:①氢原子最多发射6种频率的光子;
②氢原子从能量为E4的较高能级跃迁到能量为E1的较低能级,若真空中光速为c,则辐射的光子的波长为$\frac{hc}{{E}_{4}-{E}_{1}}$;(已知普朗克常量为h,用题目中给出的已知量表示)
③若已知E1=-13.6eV,则E4=-0.85eV.
分析 根据数学组合公式求出氢原子最多辐射不同频率光子的种数;根据辐射的光子能量等于两能级间的能级差求出辐射的光子波长.根据${E}_{n}=\frac{1}{{n}^{2}}{E}_{1}$求出第4能级的能量.
解答 解:①根据数学组合公式${C}_{4}^{2}=6$知,一群氢原子处于量子数n=4能极状态,最多辐射6种不同频率的光子.
②根据${E}_{4}-{E}_{1}=h\frac{c}{λ}$得,辐射的光子波长$λ=\frac{hc}{{E}_{4}-{E}_{1}}$.
③第4能级的能量${E}_{4}=\frac{1}{{n}^{2}}{E}_{1}=\frac{1}{16}×(-13.6)=-0.85eV$.
故答案为:①6,②$\frac{hc}{{E}_{4}-{E}_{1}}$,③-0.85.
点评 解决本题的关键知道辐射或吸收的光子能量等于两能级间的能级差,知道辐射光子波长和频率的关系,基础题.

练习册系列答案
相关题目
1.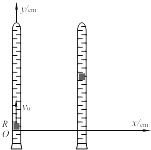 如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )
如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )
 如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )
如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )| A. | 竖直方向分位移y的平方与水平分位移x成正比 | |
| B. | 合速度v的大小随时间t均匀增加 | |
| C. | tanα与时间t成正比 | |
| D. | tanβ与时间t成正比 |
2.一个质量为2kg的物体,在5个共点作用下处于匀速直线运动状态.现同时撤去大小部分别为15N和10N的两个力,其余的力保持不变,关于此后该物体运动的情况说法中正确的是( )
| A. | 可能做匀减速直线运动,加速度大小是2m/s2 | |
| B. | 可能做匀变速圆周运动,向心加速度大小是10m/s2 | |
| C. | 该物体的速度可能先逐渐增大至某一最大值,再逐渐减小 | |
| D. | 该物体的速度可能先逐渐减小至某一非零的最小值,再逐渐增大 |
19. 如图所示,一个质量为1Kg,均匀的细链条长为2m,置于光滑水平桌面上,用手按住一端,使1m长部分垂在桌面下,(桌面高度大于链条长度,取桌面为零势能面),则链条的重力势能为( )
如图所示,一个质量为1Kg,均匀的细链条长为2m,置于光滑水平桌面上,用手按住一端,使1m长部分垂在桌面下,(桌面高度大于链条长度,取桌面为零势能面),则链条的重力势能为( )
 如图所示,一个质量为1Kg,均匀的细链条长为2m,置于光滑水平桌面上,用手按住一端,使1m长部分垂在桌面下,(桌面高度大于链条长度,取桌面为零势能面),则链条的重力势能为( )
如图所示,一个质量为1Kg,均匀的细链条长为2m,置于光滑水平桌面上,用手按住一端,使1m长部分垂在桌面下,(桌面高度大于链条长度,取桌面为零势能面),则链条的重力势能为( )| A. | -2.5 J | B. | -10 J | C. | -5 J | D. | 0 |
6.船在静水中的速度为4m/s,河岸笔直,河宽50m,适当调整船的行驶方向,使该船运动到河对岸时航程最短为L,设最短航行时间T,下列说法中正确的是( )
| A. | 当水流速度为2 m/s时,L为60 m | B. | 当水流速度为3m/s时,T为10 s | ||
| C. | 当水流速度为6 m/s时,L为75 m | D. | 当水流速度为6m/s时,T为5s |
3.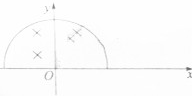 如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )
如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )
 如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )
如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )| A. | 甲粒子做圆周运动的半径$\frac{\sqrt{2}}{2}$R | |
| B. | 甲、乙粒子在磁场中运动的时间之比为3:4 | |
| C. | 甲、乙粒子的动能之比为3:1 | |
| D. | 乙粒子通过x轴的坐标为$\sqrt{3}$R |
 两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示,B与C碰撞后二者会粘在一起运动.求在以后的运动中:
两物块A、B用轻弹簧相连,质量均为2kg,初始时弹簧处于原长,A、B两物块都以v=6m/s的速度在光滑的水平地面上运动,质量4kg的物块C静止在前方,如图所示,B与C碰撞后二者会粘在一起运动.求在以后的运动中: 如图所示,在光滑水平地面上放置质量M=2kg的长木板,长木板足够长,木板上表面与固定的竖直光滑弧形轨道相切.一质量m=1kg的小滑块自A点沿弧面由静止滑下,最终和长木板一起滑行.已知A点距离长木板上表面高度h=0.45m.长木板上表面的摩擦因数为0.2.取g=10m/s2.求:
如图所示,在光滑水平地面上放置质量M=2kg的长木板,长木板足够长,木板上表面与固定的竖直光滑弧形轨道相切.一质量m=1kg的小滑块自A点沿弧面由静止滑下,最终和长木板一起滑行.已知A点距离长木板上表面高度h=0.45m.长木板上表面的摩擦因数为0.2.取g=10m/s2.求: 如图是一套热学实验装置,A容器浸没在1号烧杯的水中,可以通过电阻丝加热改变A中气体温度,B容器浸没在2号烧杯的冰水混合物中,上端用轻质绝热的活塞D封闭,活塞截面积s,上面堆有质量为m的铁砂,且$\frac{mg}{s}$=p0(大气压);A、B两容器用非常细(不计体积)的绝热管道相连,管道中有光滑轻质绝缘活塞C.已知B中气体的原来高度为l,当A中气体温度由T(热力学温度)变为3T时,求:
如图是一套热学实验装置,A容器浸没在1号烧杯的水中,可以通过电阻丝加热改变A中气体温度,B容器浸没在2号烧杯的冰水混合物中,上端用轻质绝热的活塞D封闭,活塞截面积s,上面堆有质量为m的铁砂,且$\frac{mg}{s}$=p0(大气压);A、B两容器用非常细(不计体积)的绝热管道相连,管道中有光滑轻质绝缘活塞C.已知B中气体的原来高度为l,当A中气体温度由T(热力学温度)变为3T时,求: