��Ŀ����
6�� ����Ϊ�˲�������������ʣ�����ƽ���İ�ֽ�Ϸ�һ�뾶ΪR�İ�Բ�β���ש����һ������30����������Բ��O���벣��ש��Բ���Ϸֱ��к����Ϲ�������ڰ�ֽ�ϱ�ǽ���MN��Բ��O���������ij����A��B�����߲���ש�����A��B���㵽���ߵľ���ֱ�Ϊx1��x2���ɴ˿ɵ��Ϲ��ڲ����е�������Ϊ$\frac{R}{2{x}_{2}}$����������еĴ����ٶ�Ϊc������ڸò���ש�д���ʱ��Ϊ$\frac{{R}^{2}}{2{x}_{1}c}$��
����Ϊ�˲�������������ʣ�����ƽ���İ�ֽ�Ϸ�һ�뾶ΪR�İ�Բ�β���ש����һ������30����������Բ��O���벣��ש��Բ���Ϸֱ��к����Ϲ�������ڰ�ֽ�ϱ�ǽ���MN��Բ��O���������ij����A��B�����߲���ש�����A��B���㵽���ߵľ���ֱ�Ϊx1��x2���ɴ˿ɵ��Ϲ��ڲ����е�������Ϊ$\frac{R}{2{x}_{2}}$����������еĴ����ٶ�Ϊc������ڸò���ש�д���ʱ��Ϊ$\frac{{R}^{2}}{2{x}_{1}c}$��
���� �Ϲ�������ʱȺ��Ĵ���ͬ������ǣ��Ϲ�������С���ɷ����Ϲ�������B���ɼ���֪ʶ����Ϲ�����ǵ����ң��������䶨�����Ϲ�������ʣ�ͬ��������������ʣ����ɹ�ʽv=$\frac{c}{n}$ �����ڲ���ש�д������ٶȣ�������ô�����ʱ�䣮
���  �⣺�Ϲ�������ʱȺ��Ĵ���ͬ������ǣ��Ϲ�������С����˵�֪�Ϲ�������B��
�⣺�Ϲ�������ʱȺ��Ĵ���ͬ������ǣ��Ϲ�������С����˵�֪�Ϲ�������B��
�ɼ���֪ʶ�ã��������ǵ�����ֵ sinr1=$\frac{{x}_{1}}{R}$
�����䶨�ɵ�
���������� n1=$\frac{sini}{sinr}$=$\frac{sin30��}{\frac{{x}_{1}}{R}}$=$\frac{R}{2{x}_{1}}$
ͬ���ɵ��Ϲ�������� n2=$\frac{R}{2{x}_{2}}$
����ڲ���ש�д������ٶ� v=$\frac{c}{{n}_{1}}$
����ڸò���ש�д���ʱ��Ϊ t=$\frac{R}{v}$
������� t=$\frac{{R}^{2}}{2{x}_{1}c}$
�ʴ�Ϊ��$\frac{R}{2{x}_{2}}$��$\frac{{R}^{2}}{2{x}_{1}c}$��
���� ������·ͼ���ɼ���֪ʶ�������ǵ������ǽ���Ĺؼ�����Ҫ�������䶨�ɼ�����������ٵĹ�ʽ��

��ϰ��ϵ�д�
�����Ŀ
6�� �ס�����������ͬһ�ص�ͬʱ��ʼ��ֱ���˶���v-tͼ����ͼ��ʾ������ͼ���ṩ����Ϣ��֪����˵����ȷ���ǣ�������
�ס�����������ͬһ�ص�ͬʱ��ʼ��ֱ���˶���v-tͼ����ͼ��ʾ������ͼ���ṩ����Ϣ��֪����˵����ȷ���ǣ�������
 �ס�����������ͬһ�ص�ͬʱ��ʼ��ֱ���˶���v-tͼ����ͼ��ʾ������ͼ���ṩ����Ϣ��֪����˵����ȷ���ǣ�������
�ס�����������ͬһ�ص�ͬʱ��ʼ��ֱ���˶���v-tͼ����ͼ��ʾ������ͼ���ṩ����Ϣ��֪����˵����ȷ���ǣ�������| A�� | 6 sĩ���ϼ� | |
| B�� | �����ϼ�֮ǰ���ס��������ԶΪ10 m | |
| C�� | 8 sĩ�ס��������������������������32 m | |
| D�� | ��0��4 s����4��6 s�ڼ�ƽ���ٶȴ�С��� |
11�� ��ͼ����ʾ����������Q1��Q2�̶���x���ϣ�����Q1λ��ԭ��O��a��b�����������ӳ����ϵ����㣮����һ�����������q��һ���ij��ٶ���x���a�㿪ʼ��b����Զ���˶�������ֻ�ܵ糡�����ã��������Ӿ���a��b����ʱ���ٶȷֱ�Ϊva��vb�����ٶ�������x�仯��ͼ����ͼ����ʾ���������ж���ȷ���ǣ�������
��ͼ����ʾ����������Q1��Q2�̶���x���ϣ�����Q1λ��ԭ��O��a��b�����������ӳ����ϵ����㣮����һ�����������q��һ���ij��ٶ���x���a�㿪ʼ��b����Զ���˶�������ֻ�ܵ糡�����ã��������Ӿ���a��b����ʱ���ٶȷֱ�Ϊva��vb�����ٶ�������x�仯��ͼ����ͼ����ʾ���������ж���ȷ���ǣ�������
 ��ͼ����ʾ����������Q1��Q2�̶���x���ϣ�����Q1λ��ԭ��O��a��b�����������ӳ����ϵ����㣮����һ�����������q��һ���ij��ٶ���x���a�㿪ʼ��b����Զ���˶�������ֻ�ܵ糡�����ã��������Ӿ���a��b����ʱ���ٶȷֱ�Ϊva��vb�����ٶ�������x�仯��ͼ����ͼ����ʾ���������ж���ȷ���ǣ�������
��ͼ����ʾ����������Q1��Q2�̶���x���ϣ�����Q1λ��ԭ��O��a��b�����������ӳ����ϵ����㣮����һ�����������q��һ���ij��ٶ���x���a�㿪ʼ��b����Զ���˶�������ֻ�ܵ糡�����ã��������Ӿ���a��b����ʱ���ٶȷֱ�Ϊva��vb�����ٶ�������x�仯��ͼ����ͼ����ʾ���������ж���ȷ���ǣ�������| A�� | b��ij�ǿһ��Ϊ�� | |
| B�� | Q2�������ҵ����С��Q1 | |
| C�� | a��ĵ��Ʊ�b��ĵ��Ƹ� | |
| D�� | ������a��ĵ����ܱ�b��ĵ�����С |
15��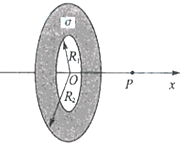 ͼʾΪһ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ���������жϣ�E�ĺ�������ʽӦΪ��������
ͼʾΪһ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ���������жϣ�E�ĺ�������ʽӦΪ��������
 ͼʾΪһ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ���������жϣ�E�ĺ�������ʽӦΪ��������
ͼʾΪһ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ���������жϣ�E�ĺ�������ʽӦΪ��������| A�� | E=2��k�ң�$\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$��x | B�� | E=2��k�ң�$\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x | ||
| C�� | E=2��k�ң�$\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x | D�� | E=2��k�ң�$\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x |

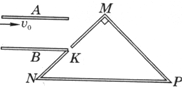 ��ͼ��ʾ��ˮƽ���õ�ƽ�н�����A��B�ļ��Ϊd�����峤Ϊ2d���������Ҳ������鵲��MN��NP��PMΧ��һ������ֱ�������������ǡ�NMP=90�㣬MN�����ϵ��е㴦��һ��С��Kǡ��λ��B���Ҷˣ���֪ˮƽ����NP�ij���Ϊ$\overline{NP}$=2$\sqrt{2}$a��������Ϊm��������Ϊ+q��ͬ��������ɵ������������ٶ�v0�ӽ�����A��B����ذ�A���ˣ������������ܵ�����������A��B����һ�㶨��ѹ��ʹ���Ӵ����������ǡ�ô�С��K����
��ͼ��ʾ��ˮƽ���õ�ƽ�н�����A��B�ļ��Ϊd�����峤Ϊ2d���������Ҳ������鵲��MN��NP��PMΧ��һ������ֱ�������������ǡ�NMP=90�㣬MN�����ϵ��е㴦��һ��С��Kǡ��λ��B���Ҷˣ���֪ˮƽ����NP�ij���Ϊ$\overline{NP}$=2$\sqrt{2}$a��������Ϊm��������Ϊ+q��ͬ��������ɵ������������ٶ�v0�ӽ�����A��B����ذ�A���ˣ������������ܵ�����������A��B����һ�㶨��ѹ��ʹ���Ӵ����������ǡ�ô�С��K����