题目内容
16.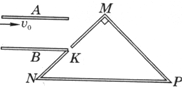 如图所示,水平放置的平行金属板A和B的间距为d,极板长为2d;金属板右侧有三块挡板MN,NP,PM围成一个等腰直角三角形区域,顶角∠NMP=90°,MN挡板上的中点处有一个小孔K恰好位于B板右端,已知水平挡板NP的长度为$\overline{NP}$=2$\sqrt{2}$a.由质量为m、带电量为+q的同种粒子组成的粒子束,以速度v0从金属板A、B左端沿板A射人,不计粒子所受的重力,若在A、B板间加一恒定电压,使粒子穿过金属板后恰好打到小孔K.求:
如图所示,水平放置的平行金属板A和B的间距为d,极板长为2d;金属板右侧有三块挡板MN,NP,PM围成一个等腰直角三角形区域,顶角∠NMP=90°,MN挡板上的中点处有一个小孔K恰好位于B板右端,已知水平挡板NP的长度为$\overline{NP}$=2$\sqrt{2}$a.由质量为m、带电量为+q的同种粒子组成的粒子束,以速度v0从金属板A、B左端沿板A射人,不计粒子所受的重力,若在A、B板间加一恒定电压,使粒子穿过金属板后恰好打到小孔K.求:(1)所施加的恒定电压大小;
(2)现允许在挡板围成的三角形区域内,加一垂直纸面的匀强磁场,要使从小孔K飞入的粒子经过磁场偏转后能直接(不与其他挡板碰撞)打到挡板MP上,求所加磁场的方向和磁感应强度的范围.
分析 (1)由题意可分析出带电粒子在两金属板间竖直方向的位移为d,水平位移为2d,水平方向上做匀速直线运动,竖直方向上做自由落体运动,运用类平抛运动的知识可求出所施加的恒定电压;
(2)根据题意,首先运用速度的合成求出带电粒子进入三角形区域时的速度,由速度方向和左手定则可得知磁场方向;再找出两个临界半径,一是带电粒子偏转轨道与NP相切时的轨道时的轨道半径,二是正好达到M点时的轨道半径,从而确定轨道半径的范围,由带电粒子在磁场中受到的洛伦兹力提供向心力$qvB=m\frac{{v}_{\;}^{2}}{R}$即可求出所加磁场的磁感应强度范围.
解答  解:(1)由于带电粒子做类平抛运动,则有:
解:(1)由于带电粒子做类平抛运动,则有:
$2d={v}_{0}^{\;}t$①
$d=\frac{1}{2}\frac{q{U}_{0}^{\;}}{md}{t}_{\;}^{2}$②
联立①②解得:${U}_{0}^{\;}=\frac{m{v}_{0}^{2}}{2q}$③
(2)设粒子在进入K时,竖直方向的分速度为${v}_{y}^{\;}$,则有:
${v}_{y}^{\;}=at=\frac{q{U}_{0}^{\;}}{md}•\frac{2d}{{v}_{0}^{\;}}={v}_{0}^{\;}$④
$tanθ=\frac{{v}_{y}^{\;}}{{v}_{0}^{\;}}=1$
得$v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{2}{v}_{0}^{\;}$⑤
可知当θ=45°时,即粒子垂直MN板射入时,要使粒子直接打到MP板上,根据左手定则,可知所加磁场的方向垂直纸面向内,如图所示,当粒子进入磁场做匀速圆周运动,偏转半径最大时恰好与NP相切;偏转半径最小时,KM为运动圆周的直径,设最大半径为${R}_{M}^{\;}$,则由几何关系可知,△NMP与$△NQ{O}_{1}^{\;}$相似,则有:
$\frac{N{O}_{1}^{\;}}{NP}=\frac{{O}_{1}^{\;}Q}{MP}$
$\frac{a+{R}_{m}^{\;}}{2\sqrt{2}a}=\frac{{R}_{m}^{\;}}{2a}$
得:${R}_{m}^{\;}=(\sqrt{2}+1)a$⑥
因此粒子做圆周运动的半径范围为:
$\frac{a}{2}<R<(\sqrt{2}+1)a$⑦
由于粒子在磁场中做圆周运动,故洛伦兹力提供向心力,即:
$qvB=m\frac{{v}_{\;}^{2}}{R}$⑧
联立⑤⑥⑦⑧式可得所加磁场的磁感应强度范围为:
$\frac{(2-\sqrt{2})m{v}_{0}^{\;}}{qa}<B<\frac{2\sqrt{2}m{v}_{0}^{\;}}{qa}$
答:(1)所施加的恒定电压大小$\frac{m{v}_{0}^{2}}{2a}$;
(2)现允许在挡板围成的三角形区域内,加一垂直纸面的匀强磁场,要使从小孔K飞入的粒子经过磁场偏转后能直接(不与其他挡板碰撞)打到挡板MP上,所加磁场的方向垂直纸面向里和磁感应强度的范围$\frac{(2-\sqrt{2})m{v}_{0}^{\;}}{qa}<B<\frac{2\sqrt{2}m{v}_{0}^{\;}}{qa}$
点评 本题考查带电粒子在电磁场中的运动,带电粒子在电场中的运动综合了静电场与力学的知识,分析方法和力学的分析方法基本相同,带电粒子在磁场中作匀速圆周运动,关键是画出临界轨迹图,运用洛伦兹力提供向心力列式求解.


| A. | A | B. | B | C. | C | D. | D |
 一边长a=20cm的正六边形处在匀强电场中,匀强电场与正六边形共面,正六边形的顶点分别为 a、b、c、d、e、f,其位置关系如图所示,已知b、d及O三点的电势分别为φb=φd=4.0V,φO=0,则以下分析正确的是( )
一边长a=20cm的正六边形处在匀强电场中,匀强电场与正六边形共面,正六边形的顶点分别为 a、b、c、d、e、f,其位置关系如图所示,已知b、d及O三点的电势分别为φb=φd=4.0V,φO=0,则以下分析正确的是( )| A. | 匀强电场的电场强度的大小为40 V/m | |
| B. | 匀强电场的方向与直线fc平行且由f指向c | |
| C. | 电子(不计重力)从O点由静止释放,一定沿线段Oc由O向c运动 | |
| D. | f点的电势φf=-8 V |
 如图所示的是表演“水流星”节目的示意图,拴杯子的绳子长为l,绳子能够承受的最大拉力是杯子和杯内水重力的8 倍,要使绳子不断,节目获得成功,则杯子通过最高点时速度的最小值和通过最低点时速度的最大值分别为( )
如图所示的是表演“水流星”节目的示意图,拴杯子的绳子长为l,绳子能够承受的最大拉力是杯子和杯内水重力的8 倍,要使绳子不断,节目获得成功,则杯子通过最高点时速度的最小值和通过最低点时速度的最大值分别为( )| A. | $\sqrt{gl}$$\sqrt{7gl}$ | B. | $\sqrt{7gl}$$\sqrt{gl}$ | C. | 0 $\sqrt{gl}$ | D. | 0 $\sqrt{7gl}$ |
 李明为了测出玻璃的折射率,他在平整的白纸上放一半径为R的半圆形玻璃砖,让一束白光以30°的入射角自圆心O射入玻璃砖,圆弧上分别有红光和紫光射出,在白纸上标记界面MN、圆心O、两光束的出射点A和B,移走玻璃砖,测得A、B两点到法线的距离分别为x1、x2.由此可得紫光在玻璃中的折射率为$\frac{R}{2{x}_{2}}$;光在真空中的传播速度为c,红光在该玻璃砖中传播时间为$\frac{{R}^{2}}{2{x}_{1}c}$.
李明为了测出玻璃的折射率,他在平整的白纸上放一半径为R的半圆形玻璃砖,让一束白光以30°的入射角自圆心O射入玻璃砖,圆弧上分别有红光和紫光射出,在白纸上标记界面MN、圆心O、两光束的出射点A和B,移走玻璃砖,测得A、B两点到法线的距离分别为x1、x2.由此可得紫光在玻璃中的折射率为$\frac{R}{2{x}_{2}}$;光在真空中的传播速度为c,红光在该玻璃砖中传播时间为$\frac{{R}^{2}}{2{x}_{1}c}$. 2007年3月1日,国家重大科学工程项引“EAST超导托卡马克核聚变实验装置“在合肥顺利通过了国家发改委组织的国家竣工验收.作为核聚变研究的实验设备,EAST可为未来的聚变反应堆进行较深入的工程和物理方面的探索,其目的是建成一个核聚变反应堆,届时从l升海水中提取氢的同位素氘.在这里和氚发生完全的核聚变反应,释放可利用能量相当于燃烧300公升汽油所获得的能量.这就相当于人类为自己制造了一个小太阳.可以得到无穷尽的清洁能源.作为核聚变研究的实验设备,要持续发生热核反应,必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内,约束的办法有多种.其中技术上相对较成熟的是用磁场约束核材料.
2007年3月1日,国家重大科学工程项引“EAST超导托卡马克核聚变实验装置“在合肥顺利通过了国家发改委组织的国家竣工验收.作为核聚变研究的实验设备,EAST可为未来的聚变反应堆进行较深入的工程和物理方面的探索,其目的是建成一个核聚变反应堆,届时从l升海水中提取氢的同位素氘.在这里和氚发生完全的核聚变反应,释放可利用能量相当于燃烧300公升汽油所获得的能量.这就相当于人类为自己制造了一个小太阳.可以得到无穷尽的清洁能源.作为核聚变研究的实验设备,要持续发生热核反应,必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内,约束的办法有多种.其中技术上相对较成熟的是用磁场约束核材料.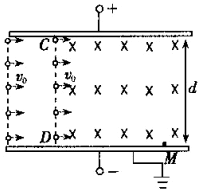 空气中的颗粒物对人体健康有重要影响.有人利用除尘器对空气除尘,除尘器主要由过滤器、离子发生器(使颗粒物带电)、集尘器组成.如图所示为集尘器的截面 图,间距为d的上、下两板与直流电源相连,CD为匀强磁场的左边界,磁场的方向垂直纸面向里.质量均为m、带相等电荷量分布均匀的颗粒物,以水平速度v0进入集尘器,调节电源电压至U,颗粒物在电场区域恰能沿水平向右做匀速直线运动,再进入电场、磁场共存区域后颗粒物偏转碰到下板后其电量消失,同时被收集,设重力加速度为g,不计颗粒物之间的相互作用.
空气中的颗粒物对人体健康有重要影响.有人利用除尘器对空气除尘,除尘器主要由过滤器、离子发生器(使颗粒物带电)、集尘器组成.如图所示为集尘器的截面 图,间距为d的上、下两板与直流电源相连,CD为匀强磁场的左边界,磁场的方向垂直纸面向里.质量均为m、带相等电荷量分布均匀的颗粒物,以水平速度v0进入集尘器,调节电源电压至U,颗粒物在电场区域恰能沿水平向右做匀速直线运动,再进入电场、磁场共存区域后颗粒物偏转碰到下板后其电量消失,同时被收集,设重力加速度为g,不计颗粒物之间的相互作用.
 如图所示,质量是M=4kg的木板静止在光滑水平面上,木板长为L0=8m,一个质量为m=1kg的小滑块以初速度V0=10m/s从左端滑上木板,由于滑块与木板间摩擦作用,木板也开始向右滑动,滑块滑到木板右端时二者恰好相对静止,求:
如图所示,质量是M=4kg的木板静止在光滑水平面上,木板长为L0=8m,一个质量为m=1kg的小滑块以初速度V0=10m/s从左端滑上木板,由于滑块与木板间摩擦作用,木板也开始向右滑动,滑块滑到木板右端时二者恰好相对静止,求: