题目内容
15.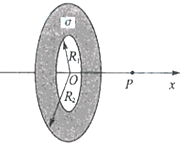 图示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.根据你的判断,E的合理表达式应为( )
图示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.根据你的判断,E的合理表达式应为( )| A. | E=2πkσ($\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$)x | B. | E=2πkσ($\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x | ||
| C. | E=2πkσ($\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x | D. | E=2πkσ($\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x |
分析 本题由于带电体为圆环状,虽然可以由微分的方式可以求得合场强,但是过程很麻烦,并超过了我们高中学生能力之外,故应注意审题,根据题意对选项进行分析,首先根据场强的单位进行判断,再利用极限的思想即可得出结论.
解答 解:场强的单位为N/C,k为静电力常量,单位为Nm2/C2,σ为单位面积的带电量,单位为C/m2,则2πkσ表达式的单位即为N/C,故各表达式中其它部分应无单位,故可知AC肯定错误;
当x=0时,此时要求的场强为O点的场强,由对称性可知EO=0,当x→∞时E→0,而D项中E→4πκσ故D项错误;所以正确选项只能为B;
故选:B
点评 本题对高中学生来说比较新颖,要求学生能应用所学过的单位制的应用及极限法;本题对学生的能力起到较好的训练作用,是道好题

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
15.如图所示,a、b两点电势相同,电场强度也相同的是( )


| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
20.细胞膜的厚度约等于800nm(1nm=10-9m),当膜的内外层间的电压达到0.4V时,即可让一价钠离子渗透.设细胞膜内的电场为匀强电场,则钠离子在渗透时( )
| A. | 膜内电场强度约为5×105V/m | |
| B. | 膜内电场强度约为2×105V/m | |
| C. | 每个钠离子沿电场方向透过膜时电场力做功约为6.4×10 -20J | |
| D. | 每个钠离子沿电场方向透过膜时电场力做功约为1.6×10 -19J |
 李明为了测出玻璃的折射率,他在平整的白纸上放一半径为R的半圆形玻璃砖,让一束白光以30°的入射角自圆心O射入玻璃砖,圆弧上分别有红光和紫光射出,在白纸上标记界面MN、圆心O、两光束的出射点A和B,移走玻璃砖,测得A、B两点到法线的距离分别为x1、x2.由此可得紫光在玻璃中的折射率为$\frac{R}{2{x}_{2}}$;光在真空中的传播速度为c,红光在该玻璃砖中传播时间为$\frac{{R}^{2}}{2{x}_{1}c}$.
李明为了测出玻璃的折射率,他在平整的白纸上放一半径为R的半圆形玻璃砖,让一束白光以30°的入射角自圆心O射入玻璃砖,圆弧上分别有红光和紫光射出,在白纸上标记界面MN、圆心O、两光束的出射点A和B,移走玻璃砖,测得A、B两点到法线的距离分别为x1、x2.由此可得紫光在玻璃中的折射率为$\frac{R}{2{x}_{2}}$;光在真空中的传播速度为c,红光在该玻璃砖中传播时间为$\frac{{R}^{2}}{2{x}_{1}c}$. 高中物理中有多个实验用到长木板轨道、实验小车、电磁打点计时器组合.现在有同学把长木板轨道调节成如图2所示的状态,完成了“探究加速度与力、质量的关系”、“探究功与速度变化的关系”实验.那么他可能获得的图象是下列的哪些图象( )
高中物理中有多个实验用到长木板轨道、实验小车、电磁打点计时器组合.现在有同学把长木板轨道调节成如图2所示的状态,完成了“探究加速度与力、质量的关系”、“探究功与速度变化的关系”实验.那么他可能获得的图象是下列的哪些图象( )



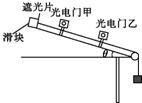 现要用如图所示的实验装置探究“动能定理”:一倾角θ可调的斜面上安装有两个光电门,其中光电门乙固定在斜面上,光电门甲的位置可移动.不可伸长的细线一端固定在带有遮光片(宽度为d)的滑块上,另一端通过光滑定滑轮与重物相连,细线与斜面平行(通过滑轮调节).当滑块沿斜面下滑时,与光电门相连的计时器可以显示遮光片挡光的时间t,从而可测出滑块通过光电门时的瞬时速度v.改变光电门甲的位置,重复实验,比较外力所做的功W与系统动能的增量△Ek的关系,即可达到实验目的.主要实验步骤如下:
现要用如图所示的实验装置探究“动能定理”:一倾角θ可调的斜面上安装有两个光电门,其中光电门乙固定在斜面上,光电门甲的位置可移动.不可伸长的细线一端固定在带有遮光片(宽度为d)的滑块上,另一端通过光滑定滑轮与重物相连,细线与斜面平行(通过滑轮调节).当滑块沿斜面下滑时,与光电门相连的计时器可以显示遮光片挡光的时间t,从而可测出滑块通过光电门时的瞬时速度v.改变光电门甲的位置,重复实验,比较外力所做的功W与系统动能的增量△Ek的关系,即可达到实验目的.主要实验步骤如下:
 2007年3月1日,国家重大科学工程项引“EAST超导托卡马克核聚变实验装置“在合肥顺利通过了国家发改委组织的国家竣工验收.作为核聚变研究的实验设备,EAST可为未来的聚变反应堆进行较深入的工程和物理方面的探索,其目的是建成一个核聚变反应堆,届时从l升海水中提取氢的同位素氘.在这里和氚发生完全的核聚变反应,释放可利用能量相当于燃烧300公升汽油所获得的能量.这就相当于人类为自己制造了一个小太阳.可以得到无穷尽的清洁能源.作为核聚变研究的实验设备,要持续发生热核反应,必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内,约束的办法有多种.其中技术上相对较成熟的是用磁场约束核材料.
2007年3月1日,国家重大科学工程项引“EAST超导托卡马克核聚变实验装置“在合肥顺利通过了国家发改委组织的国家竣工验收.作为核聚变研究的实验设备,EAST可为未来的聚变反应堆进行较深入的工程和物理方面的探索,其目的是建成一个核聚变反应堆,届时从l升海水中提取氢的同位素氘.在这里和氚发生完全的核聚变反应,释放可利用能量相当于燃烧300公升汽油所获得的能量.这就相当于人类为自己制造了一个小太阳.可以得到无穷尽的清洁能源.作为核聚变研究的实验设备,要持续发生热核反应,必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内,约束的办法有多种.其中技术上相对较成熟的是用磁场约束核材料. 如图所示,质量是M=4kg的木板静止在光滑水平面上,木板长为L0=8m,一个质量为m=1kg的小滑块以初速度V0=10m/s从左端滑上木板,由于滑块与木板间摩擦作用,木板也开始向右滑动,滑块滑到木板右端时二者恰好相对静止,求:
如图所示,质量是M=4kg的木板静止在光滑水平面上,木板长为L0=8m,一个质量为m=1kg的小滑块以初速度V0=10m/s从左端滑上木板,由于滑块与木板间摩擦作用,木板也开始向右滑动,滑块滑到木板右端时二者恰好相对静止,求: