题目内容
9.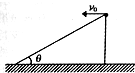 如图所示,将小球从斜面的顶点处平抛出去,且能落在斜面上.已知抛出时速度大小为v0,斜面与水平方向的夹角为θ.在小球运动过程中距离斜面最远时,其速度大小为$\frac{{v}_{0}}{cosθ}$,小球从抛出到该时所用时间为$\frac{{v}_{0}tanθ}{g}$.
如图所示,将小球从斜面的顶点处平抛出去,且能落在斜面上.已知抛出时速度大小为v0,斜面与水平方向的夹角为θ.在小球运动过程中距离斜面最远时,其速度大小为$\frac{{v}_{0}}{cosθ}$,小球从抛出到该时所用时间为$\frac{{v}_{0}tanθ}{g}$.
分析 当小球的速度方向与斜面平行时,距离斜面最远,根据平行四边形定则求出速度的大小和竖直分速度的大小,结合速度时间公式求出运动的时间.
解答 解:当小球的速度方向与斜面平行时,距离斜面最远,根据平行四边形定则知,此时的速度为:v=$\frac{{v}_{0}}{cosθ}$.
此时的竖直分速度为:vy=v0tanθ,
则小球从抛出到该时所用的时间为:t=$\frac{{v}_{y}}{g}$=$\frac{{v}_{0}tanθ}{g}$.
故答案为:$\frac{{v}_{0}}{cosθ}$,$\frac{{v}_{0}tanθ}{g}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
相关题目
19. 如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为 R,小球半径为 r,则下列说法中正确的是( )
如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为 R,小球半径为 r,则下列说法中正确的是( )
 如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为 R,小球半径为 r,则下列说法中正确的是( )
如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为 R,小球半径为 r,则下列说法中正确的是( )| A. | 小球能通过最高点时的最小速度vmin=2$\sqrt{gr}$ | |
| B. | 小球通过最高点时圆形管道对小球的弹力的最大值为 mg | |
| C. | 小球在水平线 ab以下的管道中运动时,速度越大外侧管壁对小球的弹力一定越大 | |
| D. | 小球在水平线 ab 以上的管道中运动时,速度越小内侧管壁对小球的弹力一定越小 |
17. 从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )
从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )
 从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )
从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )| A. | 甲球在空中运动的时间短 | B. | 甲、乙两球在空中运动的时间相等 | ||
| C. | 甲球平抛的初速度大 | D. | 甲、乙两球落地时速度大小相等 |
4.做匀速圆周运动的物体( )
| A. | 加速度不变 | B. | 所受到的向心力是恒力 | ||
| C. | 单位时间内位移变化相同 | D. | 单位时间内速度的变化量大小不变 |
14.某振子做简谐运动的表达式为x=4sin(5πt+6π)cm,则该振子振动的振幅和周期为( )
| A. | 4cm 6πs | B. | 4cm 5πs | C. | 4cm 0.4s | D. | 以上全错 |
1.某人造卫星运动的轨道可近似看作是以地心为中心的圆.由于阻力作用,人造卫星到地心的距离从r1慢慢变到r2,卫星的线速度增大到原来的2倍(卫星质量不变),则( )
| A. | 卫星的动能变为原来的4倍 | |
| B. | 卫星的向心加速度增大到原来的4倍 | |
| C. | 卫星的机械能保持不变 | |
| D. | 卫星的重力势能逐渐减小 |
18.质量为m的小球,从桌面上以速度v0竖直抛出,桌面离地面高为h,小球能达到的最大高度离地面为H,若以桌面为重力势能的零参考平面,不计空气阻力,则小球落地时机械能为( )
| A. | $\frac{1}{2}$mv02 | B. | $\frac{1}{2}$mv02-mgh | C. | mg(H-h) | D. | mg(H+h) |
 如图所示,一质量为m的小球,可视为质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,轻绳柔软且不可伸长,现把小球从O点的正上方离O点的距离为$\frac{3}{4}$R的O1点以水平速度v0=$\sqrt{\frac{2gR}{3}}$抛出.求:
如图所示,一质量为m的小球,可视为质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,轻绳柔软且不可伸长,现把小球从O点的正上方离O点的距离为$\frac{3}{4}$R的O1点以水平速度v0=$\sqrt{\frac{2gR}{3}}$抛出.求: