题目内容
19.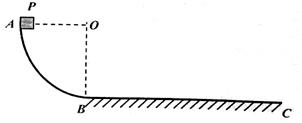 如图所示,竖直放置的光滑四分之-圆弧形轨道与足够长的粗糙水平轨道BC平滑连接.现将一质量m=1kg的滑块P(滑块的尺寸忽略不计)由A点静止释放,使其沿圆弧轨道下滑至B点,然后沿水平轨道继续向前滑行,最终停在水平轨道上的C点. 已知圆弧形轨道的半径R=0.8m,滑块与水平轨道间的动摩擦因数μ=0.1,求:
如图所示,竖直放置的光滑四分之-圆弧形轨道与足够长的粗糙水平轨道BC平滑连接.现将一质量m=1kg的滑块P(滑块的尺寸忽略不计)由A点静止释放,使其沿圆弧轨道下滑至B点,然后沿水平轨道继续向前滑行,最终停在水平轨道上的C点. 已知圆弧形轨道的半径R=0.8m,滑块与水平轨道间的动摩擦因数μ=0.1,求:(1)滑块P滑至B点时的速度大小vB;
(2)滑块P在水平轨道上滑行的距离x;
(3)若实际圆弧形轨道的摩擦不可忽略,其他已知条件不变,仍使滑块P自A点静止下沿,最终其停在水平轨道BC的中点处,求滑块P在圆弧形轨道上滑行时,克服摩擦力所做的功Wf.
分析 (1)根据滑块从A到B的运动过程机械能守恒求解;
(2)对滑块在BC轨道上运动过程应用动能定理求解即可;
(3)先求得水平轨道上摩擦力做的功,然后对从A到BC中点的运动过程应用动能定理即可.
解答 解:(1)滑块在圆弧形轨道上运动只有重力做功,故机械能守恒,所以有$mgR=\frac{1}{2}m{{v}_{B}}^{2}$
故有:${v}_{B}=\sqrt{2gR}=4m/s$;
(2)滑块在BC上运动只有摩擦力做功,故由动能定理可得:$-μmgx=0-\frac{1}{2}m{{v}_{B}}^{2}$,
解得:$x=\frac{{{v}_{B}}^{2}}{2μg}=8m$;
(3)滑块最终停在水平轨道BC的中点处,故在水平轨道上摩擦力做功为:
${W}_{f1}=-μmg•\frac{x}{2}=-4J$;
那么,滑块从A到BC中点的运动过程,只有重力、摩擦力做功,对该过程应用动能定理可得:滑块P在圆弧形轨道上滑行时,克服摩擦力所做的功为:
Wf=mgR+Wf1=4J;
答:(1)滑块P滑至B点时的速度大小vB为4m/s;
(2)滑块P在水平轨道上滑行的距离x为8m;
(3)若实际圆弧形轨道的摩擦不可忽略,其他已知条件不变,仍使滑块P自A点静止下沿,最终其停在水平轨道BC的中点处,则滑块P在圆弧形轨道上滑行时,克服摩擦力所做的功Wf为4J.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
相关题目
4.下列关于运动的说法正确的是( )
| A. | 物体做曲线运动,其合外力可能为恒力 | |
| B. | 决定平抛运动物体飞行时间的因素是初速度 | |
| C. | 做匀速圆周运动的物体,线速度和角速度都保持不变 | |
| D. | 地球上的物体随地球自转的向心加速度的大小在地球上各处都一样大 |
14.关于电势差的下列说法正确的是( )
| A. | 在电场中a、b两点的距离越大,其电势差就越大 | |
| B. | a、b两点的电势差在数值上等于单位正电荷从a点移到b点电场力所做的功 | |
| C. | 若一电荷在a、b两点的电势能相等,则这两点一定存在电势差 | |
| D. | 在匀强电场中与电场线垂直的同一平面内任意两点的电势差不为零 |
8.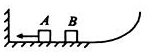 如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )
如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )
 如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )
如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )| A. | 物块A、B碰撞后瞬间的速度v=2m/s | |
| B. | 物块A、B滑上圆弧轨道的最大高度h=0.05m | |
| C. | 物块A与墙壁、物块A与B碰撞过程中,系统损失的动能之比为11:15 | |
| D. | 物块A与墙壁碰撞的过程中,墙壁对A的平均作用力的大小F=100N |
19.已知某一近地卫星绕行星运动的周期约为84分钟,引力常量G=6.67×10-11N•m2/kg2,由此估算该行星的平均密度为( )
| A. | 2.0×107kg/m3 | B. | 5.6×103kg/m3 | C. | 2.1×103kg/m3 | D. | 3.0×104kg/m3 |

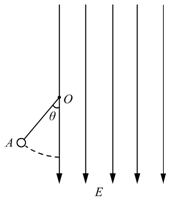 如图所示,质量m=1.0kg、带电量q=-4×10-3C的小球用长度l=0.8m的不可伸长的绝缘轻质细线悬吊在O点,过O点的竖直线右侧有竖直向下足够大的匀强电场,场强大小E=5×103N/C.现将小球拉至A处,此时,细线与竖直方向成θ角.现由静止释放小球,在小球运动过程中细线始终未被拉断.已知cosθ=$\frac{3}{4}$,取重力加速度g=10m/s2.
如图所示,质量m=1.0kg、带电量q=-4×10-3C的小球用长度l=0.8m的不可伸长的绝缘轻质细线悬吊在O点,过O点的竖直线右侧有竖直向下足够大的匀强电场,场强大小E=5×103N/C.现将小球拉至A处,此时,细线与竖直方向成θ角.现由静止释放小球,在小球运动过程中细线始终未被拉断.已知cosθ=$\frac{3}{4}$,取重力加速度g=10m/s2.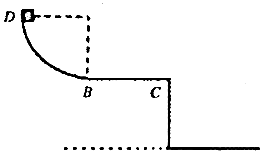 如图所示,半径为R的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B 与长为L的水平桌面相切于B点,BC离地面高为h,可视为质点的质量为m的滑块从圆 弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ,重力加速度为g,求:
如图所示,半径为R的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B 与长为L的水平桌面相切于B点,BC离地面高为h,可视为质点的质量为m的滑块从圆 弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ,重力加速度为g,求: