题目内容
4.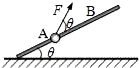 如图,一质量m=2kg的小球套在一根固定的足够长的直杆上,直杆与水平面夹角θ=37°.现小球在与杆也成θ角的斜向上F=20N的外力作用下,从A点静止出发向上运动.已知杆与球间的动摩擦因数μ=0.5,g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图,一质量m=2kg的小球套在一根固定的足够长的直杆上,直杆与水平面夹角θ=37°.现小球在与杆也成θ角的斜向上F=20N的外力作用下,从A点静止出发向上运动.已知杆与球间的动摩擦因数μ=0.5,g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)小球运动的加速度a1;
(2)若F作用4s后撤去,小球上滑过程中距A点最大距离sm.
分析 (1)对小球受力分析,运用牛顿第二定律求出小球的加速度.
(2)根据匀变速直线运动公式求出撤去拉力前的位移和末速度,再根据牛顿第二定律求出撤去拉力后的加速度,根据运动学公式求出上滑的位移,从而得出小球上滑过程中距A点最大距离.
解答 解:(1)在力F作用时有,Fcos37°-mgsin37°-μ(mg cos37°-F sin37°)=m${a}_{1}^{\;}$
代入数据:20×0.8-20×0.6-0.5(20×0.8-20×0.6)=$2{a}_{1}^{\;}$
解得:a1=1m/s2,
(2)刚撤去F时,小球的速度υ1=a1t1=1×4m/s=4m/s,
小球的位移${s_1}=\frac{v_1}{2}$t1=$\frac{4}{2}×4$=8m,
撤去力F后,小球上滑时有:-(mgsin37°+μmgcos37°)=ma2,
得:${a}_{2}^{\;}=-(gsin37°+μgcos37°)$=$-(10×0.6+0.5×10×0.8)m/{s}_{\;}^{2}$
解得:a2=-10 m/s2,
因此小球上滑时间${t_2}=\frac{{0-{v_1}}}{a_2}=0.4s$
上滑位移${s_2}=\frac{v_1}{2}$t2=$\frac{4}{2}×0.4$=0.8m,
则小球上滑的最大距离为sm=s1+s2=8.8m
答:(1)小球运动的加速度a1为1m/s2;
(2)若F作用4s后撤去,小球上滑过程中距A点最大距离sm为8.8m;
点评 牛顿第二定律和运动学公式是解决力学的基本方法.关键在于分析物体的受力情况和运动情况.当物体受力较多时,往往采用正交分解法求加速度,难度适中.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
15.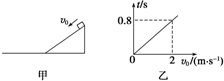 如图甲所示,用同种材料制成的倾角为30°的斜面和长水平面,斜面和水平面之间由光滑圆弧连接,斜面长为2.4m且固定.一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑.当v0=2m/s时,经过0.8s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象如图乙所示,g取10m/s2,则( )
如图甲所示,用同种材料制成的倾角为30°的斜面和长水平面,斜面和水平面之间由光滑圆弧连接,斜面长为2.4m且固定.一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑.当v0=2m/s时,经过0.8s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象如图乙所示,g取10m/s2,则( )
 如图甲所示,用同种材料制成的倾角为30°的斜面和长水平面,斜面和水平面之间由光滑圆弧连接,斜面长为2.4m且固定.一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑.当v0=2m/s时,经过0.8s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象如图乙所示,g取10m/s2,则( )
如图甲所示,用同种材料制成的倾角为30°的斜面和长水平面,斜面和水平面之间由光滑圆弧连接,斜面长为2.4m且固定.一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑.当v0=2m/s时,经过0.8s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象如图乙所示,g取10m/s2,则( )| A. | 小物块与该种材料间的动摩擦因数为0.25 | |
| B. | 小物块与该种材料间的动摩擦因数为$\frac{\sqrt{3}}{2}$ | |
| C. | 若小物块初速度为1 m/s,则根据图象可知小物块运动时间为0.4 s | |
| D. | 若小物块初速度为4 m/s,则根据图象可知小物块运动时间为1.6 s |
19. 沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )
沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )
 沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )
沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )| A. | F1>F2 | B. | F2<F3 | C. | F1>F3 | D. | F1=F3 |
14.甲物体的重量是乙物体的3倍,它们在同一高度同时自由下落,不计空气阻力,则下列说法中正确的是( )
| A. | 甲比乙先着地 | B. | 甲与乙同时着地 | ||
| C. | 甲着地时的速度比乙大 | D. | 乙着地时的速度比甲大 |
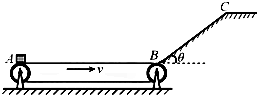 用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求:
用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求:
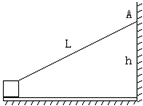 如图,厚度不计的长木板放在水平面上,并且右端紧靠竖直墙壁,木板与地面之间摩擦系数μ1=0.25,木板质量M=0.4kg,板上有一质量为m=0.3kg的小物体,与木板间摩擦系数μ2=$\frac{1}{3}$,将小物体用长为L=1m细绳系在墙上A点,A点高度h=0.6m,用水平力F=6.4N拉木板,使其从静止开始运动(此时细线是张紧的),问经多长时间小物体离开木板右端.
如图,厚度不计的长木板放在水平面上,并且右端紧靠竖直墙壁,木板与地面之间摩擦系数μ1=0.25,木板质量M=0.4kg,板上有一质量为m=0.3kg的小物体,与木板间摩擦系数μ2=$\frac{1}{3}$,将小物体用长为L=1m细绳系在墙上A点,A点高度h=0.6m,用水平力F=6.4N拉木板,使其从静止开始运动(此时细线是张紧的),问经多长时间小物体离开木板右端. 如图,在学校运动会团体托球跑步比赛中,某同学将质量为m的球置于球拍的光面中心,从静止开始先做加速度大小为a的匀加速直线运动,速度达到v0后做匀速直线运动至终点.已知运动过程中球始终相对球拍静止,且受到的空气阻力大小为f=kv(k为已知常量),方向与速度方向相反.不计球与球拍间的摩擦,重力加速度为g,求:(结果可以用三角函数表示)
如图,在学校运动会团体托球跑步比赛中,某同学将质量为m的球置于球拍的光面中心,从静止开始先做加速度大小为a的匀加速直线运动,速度达到v0后做匀速直线运动至终点.已知运动过程中球始终相对球拍静止,且受到的空气阻力大小为f=kv(k为已知常量),方向与速度方向相反.不计球与球拍间的摩擦,重力加速度为g,求:(结果可以用三角函数表示)