题目内容
10.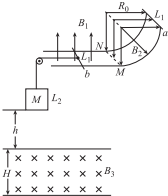 如图所示,两根等高光滑的四分之一圆弧形轨道与一足够长水平轨道相连,圆弧的半径为R0、轨道间距为L1=1m,轨道电阻不计.水平轨道处在竖直向上的匀强磁场中,磁感应强度为B1=1T,圆弧轨道处于圆心轴线上均匀向外辐射状的磁场中,如图所示.在轨道上有两长度稍大于L1、质量均为m=2kg、阻值均为R=0.5Ω的金属棒a、b,金属棒b通过跨过定滑轮的绝缘细线与一质量为M=1kg、边长为L2=0.2m、电阻r=0.05Ω的正方形金属线框相连.金属棒a从轨道最高处开始,在外力作用下以速度v0=5m/s沿轨道做匀速圆周运动到最低点MN处,在这一过程中金属棒b恰好保持静止.当金属棒a到达最低点MN处被卡住,此后金属线框开始下落,刚好能匀速进入下方h=1m处的水平匀强磁场B3中,B3=$\sqrt{5}$T.已知磁场高度H>L2.忽略一切摩擦阻力,重力加速度为g=10m/s2.求:
如图所示,两根等高光滑的四分之一圆弧形轨道与一足够长水平轨道相连,圆弧的半径为R0、轨道间距为L1=1m,轨道电阻不计.水平轨道处在竖直向上的匀强磁场中,磁感应强度为B1=1T,圆弧轨道处于圆心轴线上均匀向外辐射状的磁场中,如图所示.在轨道上有两长度稍大于L1、质量均为m=2kg、阻值均为R=0.5Ω的金属棒a、b,金属棒b通过跨过定滑轮的绝缘细线与一质量为M=1kg、边长为L2=0.2m、电阻r=0.05Ω的正方形金属线框相连.金属棒a从轨道最高处开始,在外力作用下以速度v0=5m/s沿轨道做匀速圆周运动到最低点MN处,在这一过程中金属棒b恰好保持静止.当金属棒a到达最低点MN处被卡住,此后金属线框开始下落,刚好能匀速进入下方h=1m处的水平匀强磁场B3中,B3=$\sqrt{5}$T.已知磁场高度H>L2.忽略一切摩擦阻力,重力加速度为g=10m/s2.求:(1)辐射磁场在圆弧处磁感应强度B2的大小;
(2)从金属线框开始下落到进入磁场前,金属棒a上产生的焦耳热Q;
(3)若在线框完全进入磁场时剪断细线,线框在完全离开磁场B3时刚好又达到匀速,已知线框离开磁场过程中产生的焦耳热为Q1=10.875J,则磁场的高低H为多少.
分析 (1)金属棒b做匀速直线运动,受拉力和安培力平衡,根据平衡条件列式;金属棒a做切割磁感线运动,根据切割公式和安培力列式;最后联立求解;
(2)从金属线框开始下落到进入磁场前,根据能量守恒定律列式;金属框刚好匀速进入磁场中,受重力和安培力平衡,根据平衡条件、切割公式和安培力公式列式后联立求解;
(3)从线框完全进入磁场到完全出磁场过程根据能量守恒定律列式;最后匀速离开磁场,根据平衡条件求解安培力,根据安培力公式、切割公式和欧姆定律求解末速度.
解答 解:(1)对金属棒b,由受力平衡,有:Mg=B1IL1,
右ab金属棒与导轨组成闭合回路,有:
I=$\frac{{{B_2}{L_1}{v_0}}}{2R}$,
联立方程,代入数值解得:
B2=2T;
(2)根据能量守恒定律,有:
$Mgh=\frac{1}{2}M{v^2}+\frac{1}{2}m{v^2}+2Q$
线框进入磁场的瞬间,由受力平衡,得:
Mg=B1I1L1+B3I2L2
其中:${I_1}=\frac{{{B_1}{L_1}v}}{2R}$
${I}_{2}=\frac{{B}_{3}{L}_{2}v′}{r}$,
而v′=$\sqrt{2gh}$
联立方程,代入数值解得:
Q=2J
(3)从线框完全进入磁场到完全出磁场,有:
$MgH=\frac{1}{2}Mv_1^2-\frac{1}{2}M{v^2}+{Q_1}$
在完全出磁场的瞬间,由受力平衡,得:
Mg=B3I3L2
其中:${I_3}=\frac{{{B_3}{L_2}{v_1}}}{r}$
联立方程,代入数据解得:
H=1.2m
答:(1)辐射磁场在圆弧处磁感应强度B2的大小为2T;
(2)从金属线框开始下落到进入磁场前,金属棒a上产生的焦耳热Q为2J;
(3)磁场的高低H为1.2m.
点评 本题是力电综合问题,关键是明确金属棒、金属框的受力情况和运动情况,根据能量守恒定律、安培力公式、切割公式和欧姆定律多次列式求解,不难.

| A. | 桌面受到的压力就是物体的重力 | |
| B. | 桌面受到的压力是由于它自己发生了微小形变而产生的 | |
| C. | 桌面由于发生了微小形变,从而对物体产生了竖直向上的支持力 | |
| D. | 物体由于发生了微小形变,从而对桌面产生了竖直向下的重力 |
| A. | 电场强度反映了电场力的性质,因此电场中某点的场强与试探电荷在该点所受的电场力成正比 | |
| B. | 电场中某点的场强等于$\frac{F}{q}$,但与试探电荷的受力大小及电荷量无关 | |
| C. | 电场中某点的场强方向即试探电荷在该点的受力方向 | |
| D. | 公式E=$\frac{F}{q}$和E=k$\frac{Q}{{r}^{2}}$对于任何静电场都是适用的 |
 如图所示A、B两小球质量分别为m、2m、A、B间有一被压缩了的弹簧以及一根细线相连,水平面光滑,已知弹簧弹力为F,当剪断细线瞬间两小球的加速度大小分别为aA=$\frac{F}{m}$,aB=$\frac{F}{2m}$,方向分别为aA向水平向左,aB向水平向右.
如图所示A、B两小球质量分别为m、2m、A、B间有一被压缩了的弹簧以及一根细线相连,水平面光滑,已知弹簧弹力为F,当剪断细线瞬间两小球的加速度大小分别为aA=$\frac{F}{m}$,aB=$\frac{F}{2m}$,方向分别为aA向水平向左,aB向水平向右.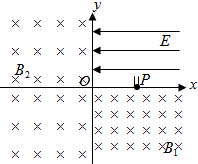 如图所示,在xoy平面的第一象限内,分布有沿x轴负方向的场强E=$\frac{4}{3}$×104N/C的匀强电场,第四象限内分布有垂直纸面向里的磁感应强度B1的匀强磁场,第二、三象限内分布有垂直纸面向里的磁感应强度B2的匀强磁场.在x轴上开有一个小孔P,距坐标原点3cm,P处连接有一段长度d=1cm内径不计,可来回抽动的准直管,管内由于静电屏蔽没有电场.粒子源S自管底部发射a粒子,假设发射的a粒速度大小v均为2×105m/s.已知a粒子带正电,比荷为$\frac{q}{m}$=5×107C/kg,重力不计,求:
如图所示,在xoy平面的第一象限内,分布有沿x轴负方向的场强E=$\frac{4}{3}$×104N/C的匀强电场,第四象限内分布有垂直纸面向里的磁感应强度B1的匀强磁场,第二、三象限内分布有垂直纸面向里的磁感应强度B2的匀强磁场.在x轴上开有一个小孔P,距坐标原点3cm,P处连接有一段长度d=1cm内径不计,可来回抽动的准直管,管内由于静电屏蔽没有电场.粒子源S自管底部发射a粒子,假设发射的a粒速度大小v均为2×105m/s.已知a粒子带正电,比荷为$\frac{q}{m}$=5×107C/kg,重力不计,求: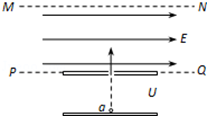 如图所示,虚线PQ、MN间存在水平匀强电场,一带电粒子质量为m=2.0×10-11kg、电荷量为q=+1.0×10-5C,从a点由静止开始经电压为U=100V的电场加速后,垂直于匀强电场进入匀强电场中,从虚线MN的某点b(图中未画出)离开匀强电场时速度与电场方向成30°角.已知PQ、MN间距为20cm,带电粒子的重力忽略不计.求:
如图所示,虚线PQ、MN间存在水平匀强电场,一带电粒子质量为m=2.0×10-11kg、电荷量为q=+1.0×10-5C,从a点由静止开始经电压为U=100V的电场加速后,垂直于匀强电场进入匀强电场中,从虚线MN的某点b(图中未画出)离开匀强电场时速度与电场方向成30°角.已知PQ、MN间距为20cm,带电粒子的重力忽略不计.求: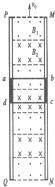 如图所示,在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直轨道平面交替排列的匀强磁场B1和B2,B1=B2=1.0T,B1和B2的方向相反,两磁场始终竖直向上做匀速运动.垂直轨道有一金属框abcd,并且与之绝缘.已知金属框的总质量为4.75×103kg,运动时所受阻力f=500N,金属框垂直轨道的边长Lcd=2.0m,两磁场的宽度均与金属框的边长Lad相同,金属框整个回路的电阻R=9.0×10-4Ω,g取10m/s2.假如金属框以v1=10m/s的速度匀速上升,求:
如图所示,在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直轨道平面交替排列的匀强磁场B1和B2,B1=B2=1.0T,B1和B2的方向相反,两磁场始终竖直向上做匀速运动.垂直轨道有一金属框abcd,并且与之绝缘.已知金属框的总质量为4.75×103kg,运动时所受阻力f=500N,金属框垂直轨道的边长Lcd=2.0m,两磁场的宽度均与金属框的边长Lad相同,金属框整个回路的电阻R=9.0×10-4Ω,g取10m/s2.假如金属框以v1=10m/s的速度匀速上升,求: 如图所示,A板和B板为平行板电容器的两极板,其中A板带负电,B板带正电,两极板的中央都有一个小空隙可以允许粒子穿过,两板间的电势差的大小为U=1×105V,B极板的右上方存在着一个圆心为O1的圆柱形匀强磁场区域,磁感应强度B=0.10T,磁场区域半径r=$\frac{2}{3}$$\sqrt{3}$m,磁场的方向垂直于纸面向里.今有质量m=3.2×10-26kg、带电荷量q=-1.6×10-19C的某种粒子,从A极板小孔处极小的初速度(其方向由A到B,大小可以视为零)进入两平行金属板之间的区域.图中A、B板上的两个小孔和O1三点共线.粒子穿越圆柱形磁场后恰好从磁场区域的最右端C点穿出,立即进入一个竖直方向的有界匀强电场,其左右边界分别为DE和FH,两边界间的距离 为8m,上边和下边没有边界.匀强电场的场强大小为E=3.75×104N/C,方向在竖直方向上.试求:
如图所示,A板和B板为平行板电容器的两极板,其中A板带负电,B板带正电,两极板的中央都有一个小空隙可以允许粒子穿过,两板间的电势差的大小为U=1×105V,B极板的右上方存在着一个圆心为O1的圆柱形匀强磁场区域,磁感应强度B=0.10T,磁场区域半径r=$\frac{2}{3}$$\sqrt{3}$m,磁场的方向垂直于纸面向里.今有质量m=3.2×10-26kg、带电荷量q=-1.6×10-19C的某种粒子,从A极板小孔处极小的初速度(其方向由A到B,大小可以视为零)进入两平行金属板之间的区域.图中A、B板上的两个小孔和O1三点共线.粒子穿越圆柱形磁场后恰好从磁场区域的最右端C点穿出,立即进入一个竖直方向的有界匀强电场,其左右边界分别为DE和FH,两边界间的距离 为8m,上边和下边没有边界.匀强电场的场强大小为E=3.75×104N/C,方向在竖直方向上.试求: