题目内容
16．
在倾角为30°的光滑斜面上放着一个质量M=2kg的物体A，由轻绳与质量为m的物体B相连，如图所示，A和B都处于静止状态，（g取10N/kg）求：（1）A所受的支持力大小；
（2）绳子的拉力大小；
（3）B物体的质量．
分析 由题，AB均处于静止状态，合力均为零，将A所受的重力分解，由平衡条件求得绳子的拉力大小，再对B，分析受力，由平衡条件求出B的质量．
解答 解：（1）A受重力、支持力、拉力，三力平衡，将A物体所受的重力分解为沿斜面向下的分力GA1和垂直斜面向下的GA2，
则 GA1=Mgsin30°，GA2=Mgcos30°；
A所受的支持力大小FN=GA2=Mgcos30°=2×$10×\frac{\sqrt{3}}{2}$=10$\sqrt{3}$N；
（2）绳子对A物的拉力：T=GA1=Mgsin30°=2×$10×\frac{1}{2}$=10N；
（3）对于物体B：绳子拉力T与重力GB平衡，因此 GB=T，
由于：GB=mg，
解得m=1kg；
答：（1）A所受的支持力大小为10$\sqrt{3}$N；
（2）绳子的拉力大小为10N；
（3）B物体的质量为1kg．
点评 本题是简单的连接体平衡问题，采用隔离法进行研究，分析受力是解题的关键．
练习册系列答案
相关题目
6．
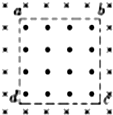如图所示，边长为L的正方形abcd为两个匀强磁场的边界，正方形内磁场的方向垂直纸面向外．磁感应强度大小为B，正方形外的磁场范围足够大，方向垂直纸面向里、磁感应强度大小也为B；把一个离子源放在顶点a处，它将沿ac连线方向发射质量也为m、电荷量为q（q＞0）、初速度为v0=$\frac{\sqrt{2}qBL}{2m}$的带负电粒子（重力不计），下列说法正确的是（ ）
如图所示，边长为L的正方形abcd为两个匀强磁场的边界，正方形内磁场的方向垂直纸面向外．磁感应强度大小为B，正方形外的磁场范围足够大，方向垂直纸面向里、磁感应强度大小也为B；把一个离子源放在顶点a处，它将沿ac连线方向发射质量也为m、电荷量为q（q＞0）、初速度为v0=$\frac{\sqrt{2}qBL}{2m}$的带负电粒子（重力不计），下列说法正确的是（ ）| A． | 粒子在磁场中做匀速圆周运动的半径为$\sqrt{2}$L | |
| B． | 粒子在磁场中做匀速圆周运动的周期为$\frac{2πm}{qB}$ | |
| C． | 粒子第一次到达c点所用的时间为$\frac{πm}{qB}$ | |
| D． | 粒子第一次返回a点所用的时间为$\frac{4πm}{qB}$ |
7．关于自由落体运动（g=10m/s2），下列说法不正确的是（ ）
| A． | 它是竖直向下，v0=0、a=g的匀加速直线运动 | |
| B． | 在开始连续三个2秒内通过的位移之比是1：3：5 | |
| C． | 在开始连续的三个2秒末的速度大小之比是1：2：3 | |
| D． | 从开始运动到距下落点4m，8m，12m所经历的时间内的平均速度的比为1：2：3 |
8．如图所示，两个可视为质点的、相同的木块A和B放在转盘上，两者用长为L的细绳连接，木块与转盘的最大静摩擦力均为各自重力的K倍，A放在距离转轴L处，整个装置能绕通过转盘中心的转轴O1O2转动．开始时，绳恰好伸直但无弹力，现让该装置从静止开始转动，使角速度缓慢增大，以下说法不正确的是（ ）
| A． | 当ω＞$\sqrt{\frac{2Kg}{3L}}$ 时，A、B相对于转盘会滑动 | |
| B． | 当ω＞$\sqrt{\frac{Kg}{2L}}$ 时，绳子一定有弹力 | |
| C． | ω在$\sqrt{\frac{Kg}{2L}}$＜ω＜$\sqrt{\frac{2Kg}{3L}}$范围内增大时，B所受摩擦力变大 | |
| D． | ω在0＜ω＜$\sqrt{\frac{2Kg}{3L}}$范围内增大时，A所受摩擦力一直变大 |
表示）的伏安特性曲线．要求所测电压范围为0.1～4V．现有器材：直流电源E（电动势4V、内阻不计），电压表
（量程4.5V，内阻约为4×104Ω），电流表
（量程250mA，内阻约为2Ω），电流表
（量程为500mA，内阻约为1Ω），滑动变阻器R（最大阻值约为30Ω），电键S，导线若干．
