题目内容
8.如图所示,两个可视为质点的、相同的木块A和B放在转盘上,两者用长为L的细绳连接,木块与转盘的最大静摩擦力均为各自重力的K倍,A放在距离转轴L处,整个装置能绕通过转盘中心的转轴O1O2转动.开始时,绳恰好伸直但无弹力,现让该装置从静止开始转动,使角速度缓慢增大,以下说法不正确的是( )
| A. | 当ω>$\sqrt{\frac{2Kg}{3L}}$ 时,A、B相对于转盘会滑动 | |
| B. | 当ω>$\sqrt{\frac{Kg}{2L}}$ 时,绳子一定有弹力 | |
| C. | ω在$\sqrt{\frac{Kg}{2L}}$<ω<$\sqrt{\frac{2Kg}{3L}}$范围内增大时,B所受摩擦力变大 | |
| D. | ω在0<ω<$\sqrt{\frac{2Kg}{3L}}$范围内增大时,A所受摩擦力一直变大 |
分析 开始角速度较小,两木块都靠静摩擦力提供向心力,B先到达最大静摩擦力,角速度继续增大,则绳子出现拉力,角速度继续增大,A的静摩擦力增大,当增大到最大静摩擦力时,开始发生相对滑动.
解答 解:A、当A所受的摩擦力达到最大静摩擦力时,A、B相对于转盘会滑动,对A有:kmg-T=mLω2,对B有:T+kmg=m•2Lω2,解得ω=$\sqrt{\frac{2Kg}{3L}}$,
当ω>$\sqrt{\frac{2Kg}{3L}}$时,A、B相对于转盘会滑动.故A正确.
B、当B达到最大静摩擦力时,绳子开始出现弹力,kmg=m•2Lω2,
解得ω1=$\sqrt{\frac{Kg}{2L}}$,知ω>$\sqrt{\frac{Kg}{2L}}$时,绳子具有弹力.故B正确.
C、角速度0<ω<$\sqrt{\frac{Kg}{2L}}$,B所受的摩擦力变大,ω在$\sqrt{\frac{Kg}{2L}}$<ω<$\sqrt{\frac{2Kg}{3L}}$范围内增大时,B所受摩擦力不变.故C错误.
D、当ω在0<ω<$\sqrt{\frac{2Kg}{3L}}$,范围内增大时,A所受摩擦力一直增大.故D正确.
本题选错误的
故选:C
点评 解决本题的关键搞清木块向心力的来源,结合牛顿第二定律进行分析,知道当A的静摩擦力增大到最大静摩擦力时,开始发生相对滑动,难度适中.

练习册系列答案
相关题目
3. 如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )
如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )
 如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )
如图所示,一小滑块(可视为质点)沿足够长的斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经B、C时的速度分别为vB、vC,则( )| A. | vC=3 m/s | B. | vB=$\sqrt{8}$ m/s | ||
| C. | DE=3 m | D. | 从D到E所用时间为4 s |
20. A、B、C三质点同时同地沿一直线运动,其s-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
A、B、C三质点同时同地沿一直线运动,其s-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
 A、B、C三质点同时同地沿一直线运动,其s-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
A、B、C三质点同时同地沿一直线运动,其s-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )| A. | 三质点的位移大小相等 | B. | 质点C的平均速度最小 | ||
| C. | 质点A的位移最大 | D. | 三质点平均速度一定不相等 |
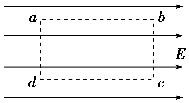 如图所示的匀强电场场强为103 N/C,沿电场线方向ab=dc=4cm垂直电场线方向bc=ad=3cm.则ab之间的电势差为40V,若将q=-5×10-3 C的点电荷沿矩形路径abcd移动一周,电场力做功是0J.
如图所示的匀强电场场强为103 N/C,沿电场线方向ab=dc=4cm垂直电场线方向bc=ad=3cm.则ab之间的电势差为40V,若将q=-5×10-3 C的点电荷沿矩形路径abcd移动一周,电场力做功是0J.
 在倾角为30°的光滑斜面上放着一个质量M=2kg的物体A,由轻绳与质量为m的物体B相连,如图所示,A和B都处于静止状态,(g取10N/kg)求:
在倾角为30°的光滑斜面上放着一个质量M=2kg的物体A,由轻绳与质量为m的物体B相连,如图所示,A和B都处于静止状态,(g取10N/kg)求: 在做“验证力的平行四边形定则”实验时,
在做“验证力的平行四边形定则”实验时,
