题目内容
14.地球的半径为R,地球表面处的重力加速度为g,一颗人造卫星围绕地球做匀速圆周运动,卫星距地面的高度为R,下列关于卫星的说法中正确的是( )| A. | 卫星的速度大小为$\frac{{\sqrt{2gR}}}{2}$ | B. | 卫星的角速度大小$\sqrt{\frac{g}{8R}}$ | ||
| C. | 卫星的加速度大小为 $\frac{g}{2}$ | D. | 卫星的运动周期为2π$\sqrt{\frac{2R}{g}}$ |
分析 在地球表面重力与万有引力相等,人造地球卫星圆周运动的向心力由万有引力提供,据此列式分析即可.
解答 解:在地球表面有:$G\frac{mM}{{R}^{2}}=mg$可得:GM=gR2
卫星的轨道半径r=R+R=2R,由万有引力提供圆周运动向心力有:
$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}=mr{ω}^{2}=ma=mr\frac{4{π}^{2}}{{T}^{2}}$由此可判断:
A:卫星的线速度$v=\sqrt{\frac{GM}{r}}$=$\sqrt{\frac{g{R}^{2}}{2R}}=\frac{\sqrt{2gR}}{2}$,故A正确;
B:卫星的角速度$ω=\sqrt{\frac{GM}{{r}^{3}}}=\sqrt{\frac{g{R}^{2}}{(2R)^{3}}}=\sqrt{\frac{g}{8R}}$,故B正确;
C、卫星的加速度$a=\frac{GM}{{r}^{2}}=\frac{g{R}^{2}}{(2R)^{2}}=\frac{g}{4}$,故C错误;
D、卫星运动的周期T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}=2π\sqrt{\frac{(2R)^{3}}{g{R}^{2}}}=4π\sqrt{\frac{2R}{g}}$,故D错误.
故选:AB.
点评 解决本题的思路主要有:一是星球表面重力与万有引力相等,二是万有引力提供卫星圆周运动的向心力.注意掌握万有引力及向心力的不同表达式是正确解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
19.宇宙中两个相距较近的星球可以看成双星,它们只在相互间的万有引力作用下,绕两球心连线上的某一固定点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法正确的是( )
| A. | 双星做圆周运动的动能均减小 | B. | 双星做圆周运动的半径均增大 | ||
| C. | 双星相互间的万有引力变大 | D. | 双星做圆周运动的周期均增大 |
6.请读下面诗词:“锄禾日当午,汗滴禾下土”.在汗水下落过程中,不计空气阻力,下列说法正确的是( )
| A. | 机械能减少 | B. | 机械能增加 | C. | 重力势能减少 | D. | 重力势能增加 |
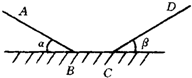 如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求:
如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求:
 轻质弹簧原长为2R,将弹簧竖直放置在地面上,将一质量为6m的物体置于弹簧的顶端由静止释放,当弹簧被压缩到最短时,弹簧长度为R.现将该弹簧放置在倾角为370的斜面轨道AC上,一端固定在斜面下端挡板上的A点,另一端与物块P接触但不连接.直轨道与一半径为R的光滑圆弧轨道相切于C点,AC=6R,A、B、C、D均在同一竖直面内.用外力推动物块P,将弹簧压缩长度R后,此时物块P位于B处,如图所示.撤去外力释放物块P,P开始沿轨道运动,重力加速度为g,物块P与BC间的动摩擦因数μ=0.5.(取sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)
轻质弹簧原长为2R,将弹簧竖直放置在地面上,将一质量为6m的物体置于弹簧的顶端由静止释放,当弹簧被压缩到最短时,弹簧长度为R.现将该弹簧放置在倾角为370的斜面轨道AC上,一端固定在斜面下端挡板上的A点,另一端与物块P接触但不连接.直轨道与一半径为R的光滑圆弧轨道相切于C点,AC=6R,A、B、C、D均在同一竖直面内.用外力推动物块P,将弹簧压缩长度R后,此时物块P位于B处,如图所示.撤去外力释放物块P,P开始沿轨道运动,重力加速度为g,物块P与BC间的动摩擦因数μ=0.5.(取sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)