题目内容
4.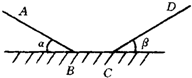 如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求:
如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求:(1)滑块在A和D点所具有的重力势能是多少?(以BC面为零势面)
(2)BC面的动摩擦因数;
(3)滑块最终停在BC面上什么位置?
分析 (1)以BC面为零势面,根据A点和D点相对于BC的高度,求重力势能.
(2)对A到D的过程运用动能定理,抓住动能的变化量为零,求出滑块与BC面的动摩擦因数.
(3)对全过程运用动能定理求出滑块在BC面上运行的总路程,从而确定滑块最终停止的位置.
解答 解:(1)由题,sAB=100cm=1m,sCD=60cm=0.6m,sBC=28cm=0.28m
滑块在A和D点所具有的重力势能分别为:
EPA=mgsABsinα=10J
EPD=mgsCDsinβ=7.2J
(2)滑块在A到D的过程中,由动能定理得:
mg(sABsinα-sCDsinβ)-μmg•sBC=0
代入数据解得:μ=0.5
(3)设滑块在BC上运动的总路程为s,由A点到最后停止的整个过程,由动能定理得:
mgsABsinα-μmg•sBC=0
代入数据解得:s=1m
因为 $\frac{s}{{s}_{BC}}$=$\frac{1}{0.28}$=3$\frac{4}{7}$
所以滑块最终停在距C点的距离为:
x=s-3sBC=1-0.84=0.16m=16cm
答:(1)滑块在A和D点所具有的重力势能分别是10J和7.2J.
(2)BC面的动摩擦因数是0.5;
(3)滑块最终停在距C点16cm处.
点评 本题考查了动能定理的基本运用,运用动能定理解题,关键选择好研究的过程,判断在该过程中有哪些力做功,然后根据动能定理列式求解.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
14. 如图所示,一物块从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.测得每隔3s的三个时刻物体的瞬时速度,记录在下表中.g取10m/s2,
如图所示,一物块从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.测得每隔3s的三个时刻物体的瞬时速度,记录在下表中.g取10m/s2,
(1)求AB和BC段所用的时间;
(2)求B点速度;
(3)求AB段和BC段的距离.
 如图所示,一物块从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.测得每隔3s的三个时刻物体的瞬时速度,记录在下表中.g取10m/s2,
如图所示,一物块从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.测得每隔3s的三个时刻物体的瞬时速度,记录在下表中.g取10m/s2,| t/s | 0 | 3 | 6 | 9 |
| v(m/s) | 0 | 8 | 12 | 8 |
(2)求B点速度;
(3)求AB段和BC段的距离.
15.已知万有引力常量G,地球半径R,月球和地球之间的距离r,地球同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g.根据以上条件,正确计算地球质量M的关系式是( )
| A. | $M=\frac{{4{π^2}{h^3}}}{{G{T_2}^2}}$ | B. | $M=\frac{{g{R^2}}}{G}$ | ||
| C. | $M=\frac{{4{π^2}{r^3}}}{{G{T_1}^2}}$ | D. | $M=\frac{{4{π^2}{{(R+h)}^3}}}{{G{T_2}^2}}$ |
19.跳伞表演是观赏性很强体育项目.当运动员从直升飞机由静止跳下后,在下落过程中会受到水平风力的影响.下列说法中正确的是( )
| A. | 风力越大,运动员下落时间越短 | B. | 风力越大,运动员着地速度越小 | ||
| C. | 运动员下落时间与风力无关 | D. | 运动员着地速度与风力无关 |
16. 一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )
一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )
 一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )
一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )| A. | 动能减小了$\frac{3}{4}$mgh | B. | 重力势能减少了mgh | ||
| C. | 机械能损失了$\frac{1}{2}$mgh | D. | 物体克服摩擦力做功$\frac{1}{4}$mgh |
13. 如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动一段距离.在此过程中( )
如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动一段距离.在此过程中( )
 如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动一段距离.在此过程中( )
如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动一段距离.在此过程中( )| A. | 外力F做的功等于A和B动能的增量 | |
| B. | B对A的摩擦力所做的功,等于A的动能增量 | |
| C. | A对B的摩擦力所做的功,等于B对A的摩擦力所做的功 | |
| D. | 外力F对B做的功等于B的动能的增量 |
14.地球的半径为R,地球表面处的重力加速度为g,一颗人造卫星围绕地球做匀速圆周运动,卫星距地面的高度为R,下列关于卫星的说法中正确的是( )
| A. | 卫星的速度大小为$\frac{{\sqrt{2gR}}}{2}$ | B. | 卫星的角速度大小$\sqrt{\frac{g}{8R}}$ | ||
| C. | 卫星的加速度大小为 $\frac{g}{2}$ | D. | 卫星的运动周期为2π$\sqrt{\frac{2R}{g}}$ |
 如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体接触(未连接),弹簧水平且无形变.用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止.撤去F后,物体开始向左运动,运动的最大距离为4x0.物体与水平面间的动摩擦因数为 μ,重力加速度为g.求:
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体接触(未连接),弹簧水平且无形变.用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止.撤去F后,物体开始向左运动,运动的最大距离为4x0.物体与水平面间的动摩擦因数为 μ,重力加速度为g.求: