题目内容
19.宇宙中两个相距较近的星球可以看成双星,它们只在相互间的万有引力作用下,绕两球心连线上的某一固定点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法正确的是( )| A. | 双星做圆周运动的动能均减小 | B. | 双星做圆周运动的半径均增大 | ||
| C. | 双星相互间的万有引力变大 | D. | 双星做圆周运动的周期均增大 |
分析 双星做匀速圆周运动具有相同的角速度,靠相互间的万有引力提供向心力,应用万有引力定律与牛顿第二定律求出双星的轨道半径关系,从而确定出双星的半径如何变化,以及得出双星的角速度和周期的变化.
解答 解:根据万有引力提供向心力,双星做匀速圆周运动具有相同的角速度和周期,$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{1}^{\;}={m}_{2}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{2}^{\;}$,得${m}_{1}^{\;}{r}_{1}^{\;}={m}_{2}^{\;}{r}_{2}^{\;}$,且${r}_{1}^{\;}+{r}_{2}^{\;}=L$,得${r}_{1}^{\;}=\frac{{m}_{2}^{\;}}{{m}_{1}^{\;}+{m}_{2}^{\;}}L$,${r}_{2}^{\;}=\frac{{m}_{1}^{\;}}{{m}_{1}^{\;}+{m}_{2}^{\;}}L$
A、根据万有引力提供向心力,$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}\frac{{v}_{1}^{2}}{{r}_{1}^{\;}}$,即${E}_{k1}^{\;}=\frac{1}{2}{m}_{1}^{\;}{v}_{1}^{2}=G\frac{{m}_{1}^{\;}{m}_{2}^{\;}{r}_{1}^{\;}}{2{L}_{\;}^{2}}$=$G\frac{{m}_{1}^{\;}{m}_{2}^{2}}{2L({m}_{1}^{\;}+{m}_{2}^{\;})}$,
同理$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{2}^{\;}\frac{{v}_{2}^{2}}{{r}_{2}^{\;}}$,即${E}_{k2}^{\;}=\frac{1}{2}{m}_{2}^{\;}{v}_{2}^{2}=G\frac{{m}_{1}^{\;}{m}_{2}^{\;}{r}_{2}^{\;}}{2{L}_{\;}^{2}}$=$G\frac{{m}_{1}^{2}{m}_{2}^{\;}}{2L({m}_{1}^{\;}+{m}_{2}^{\;})}$,因为双星距离增大知双星做圆周运动的动能均减小,故A正确
B、根据万有引力提供向心力,$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{1}^{\;}={m}_{2}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{2}^{\;}$,得${m}_{1}^{\;}{r}_{1}^{\;}={m}_{2}^{\;}{r}_{2}^{\;}$,且${r}_{1}^{\;}+{r}_{2}^{\;}=L$,得${r}_{1}^{\;}=\frac{{m}_{2}^{\;}}{{m}_{1}^{\;}+{m}_{2}^{\;}}L$,${r}_{2}^{\;}=\frac{{m}_{1}^{\;}}{{m}_{1}^{\;}+{m}_{2}^{\;}}L$,由题意知双星间距离增加,双星做圆周运动的半径均增大,故B正确;
C、双星间的距离在缓慢增大,根据万有引力定律$F=G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{r}_{\;}^{2}}$,知万有引力减小,故C错误;
D、根据$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{1}^{\;}={m}_{2}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{2}^{\;}$,得${m}_{1}^{\;}=\frac{4{π}_{\;}^{2}{r}_{2}^{\;}{L}_{\;}^{2}}{G{T}_{\;}^{2}}$,${m}_{2}^{\;}=\frac{4{π}_{\;}^{2}{r}_{1}^{\;}{L}_{\;}^{2}}{G{T}_{\;}^{2}}$,${m}_{1}^{\;}+{m}_{2}^{\;}=\frac{4{π}_{\;}^{2}{L}_{\;}^{3}}{G{T}_{\;}^{2}}$,得$T=\sqrt{\frac{4{π}_{\;}^{2}{L}_{\;}^{3}}{G({m}_{1}^{\;}+{m}_{2}^{\;})}}$,因为双星间距离增大,双星做圆周运动的周期均增大,故D正确;
故选:ABD
点评 解决本题的关键知道双星靠相互间的万有引力提供向心力,应用万有引力定律与牛顿第二定律即可正确解题,知道双星的轨道半径比等于质量之反比

 如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )
如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )| A. | 在该过程中,物块的运动是加速的 | |
| B. | 在该过程中,人对物块做的功为$\frac{{m{v^2}{x^2}}}{{2({h^2}+{x^2})}}$ | |
| C. | 在该过程中,人对物块做的功为$\frac{1}{2}m{v^2}$ | |
| D. | 人前进x时,物块的运动速率为$\frac{vx}{{\sqrt{{x^2}+{h^2}}}}$ |
| A. | 卫星的速度大小为$\frac{{\sqrt{2gR}}}{2}$ | B. | 卫星的角速度大小$\sqrt{\frac{g}{8R}}$ | ||
| C. | 卫星的加速度大小为 $\frac{g}{2}$ | D. | 卫星的运动周期为2π$\sqrt{\frac{2R}{g}}$ |
| A. | 两条细绳必须等长 | |
| B. | 弹簧测力计、细绳、橡皮条都应与木板平面平行 | |
| C. | 拉橡皮条的细绳要稍长一些,标记同一条细绳的方向时两标记点要适当远一些 | |
| D. | 实验前先把实验所用的两只弹簧测力计的挂钩相互钩住平放在桌面上,向相反方向拉动,检查读数是否相同,若不同,则进行调节使之相同 |
 如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体接触(未连接),弹簧水平且无形变.用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止.撤去F后,物体开始向左运动,运动的最大距离为4x0.物体与水平面间的动摩擦因数为 μ,重力加速度为g.求:
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体接触(未连接),弹簧水平且无形变.用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止.撤去F后,物体开始向左运动,运动的最大距离为4x0.物体与水平面间的动摩擦因数为 μ,重力加速度为g.求: 在“研究平抛物体的运动”的实验中,某同学在平抛运动轨迹上选取A、B两点,现测得A点的速度方向与水平方向的夹角为30°,B点的速度方向与水平方向的夹角为60°.从抛出点分別到A、B点的水平位移之比为1:3;从抛出点分别到A、B点的竖直位移之比为1:9.
在“研究平抛物体的运动”的实验中,某同学在平抛运动轨迹上选取A、B两点,现测得A点的速度方向与水平方向的夹角为30°,B点的速度方向与水平方向的夹角为60°.从抛出点分別到A、B点的水平位移之比为1:3;从抛出点分别到A、B点的竖直位移之比为1:9.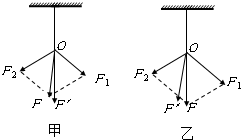 (1)在做“探究合力与分力关系”的实验时,橡皮条的一端固定在木板上,用两个弹簧秤把橡皮条的另一端拉到某一确定的O点,则下列说法中正确的是AB
(1)在做“探究合力与分力关系”的实验时,橡皮条的一端固定在木板上,用两个弹簧秤把橡皮条的另一端拉到某一确定的O点,则下列说法中正确的是AB  如图甲所示,直线AB是某电场中的一条电场线,一电子仅在电场力作用下由电场线上A点沿直线运动到B点,其速度平方v2与位移x的关系如图乙所示,EA、EB表示A、B两点的电场强度,φA、φB表示A、B两点的电势.以下判断正确的是( )
如图甲所示,直线AB是某电场中的一条电场线,一电子仅在电场力作用下由电场线上A点沿直线运动到B点,其速度平方v2与位移x的关系如图乙所示,EA、EB表示A、B两点的电场强度,φA、φB表示A、B两点的电势.以下判断正确的是( )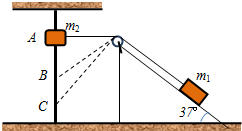 如图所示,一轻绳跨过光滑的小定滑轮,一端与在倾角为37°的光滑斜面上的小物体m1连接,另一端与套在光滑竖直杆上的小物体m2连接,滑轮到竖直杆的距离为1.2m.现在让物体m2从与滑轮等高的A点由静止释放,设斜面和杆足够长,m1不会碰到滑轮,m2不会碰到地面,g取10m/s2.
如图所示,一轻绳跨过光滑的小定滑轮,一端与在倾角为37°的光滑斜面上的小物体m1连接,另一端与套在光滑竖直杆上的小物体m2连接,滑轮到竖直杆的距离为1.2m.现在让物体m2从与滑轮等高的A点由静止释放,设斜面和杆足够长,m1不会碰到滑轮,m2不会碰到地面,g取10m/s2.