题目内容
2. 轻质弹簧原长为2R,将弹簧竖直放置在地面上,将一质量为6m的物体置于弹簧的顶端由静止释放,当弹簧被压缩到最短时,弹簧长度为R.现将该弹簧放置在倾角为370的斜面轨道AC上,一端固定在斜面下端挡板上的A点,另一端与物块P接触但不连接.直轨道与一半径为R的光滑圆弧轨道相切于C点,AC=6R,A、B、C、D均在同一竖直面内.用外力推动物块P,将弹簧压缩长度R后,此时物块P位于B处,如图所示.撤去外力释放物块P,P开始沿轨道运动,重力加速度为g,物块P与BC间的动摩擦因数μ=0.5.(取sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)
轻质弹簧原长为2R,将弹簧竖直放置在地面上,将一质量为6m的物体置于弹簧的顶端由静止释放,当弹簧被压缩到最短时,弹簧长度为R.现将该弹簧放置在倾角为370的斜面轨道AC上,一端固定在斜面下端挡板上的A点,另一端与物块P接触但不连接.直轨道与一半径为R的光滑圆弧轨道相切于C点,AC=6R,A、B、C、D均在同一竖直面内.用外力推动物块P,将弹簧压缩长度R后,此时物块P位于B处,如图所示.撤去外力释放物块P,P开始沿轨道运动,重力加速度为g,物块P与BC间的动摩擦因数μ=0.5.(取sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)(1)若物块P的质量为m,求物块P到达C点时速度的大小;
(2)改变物块P的质量,再用外力将物块P仍推至B 点,静止释放后,若物块 P沿轨道运动至圆弧的最高点D处水平飞出后,恰好通过与C在同一水平高度上的E点,E点与C点水平相距$\frac{21}{5}$R,求物块P运动到D点时速度的大小及改变后物块P的质量.
分析 (1)将6m的物体置于弹簧的顶端由静止释放,由系统的机械能守恒求出弹簧的弹性势能.若物块P的质量为m,在外力作用下,P将弹簧压缩长度R时,弹簧的弹性势能不变.P由B到达C点,运用动能定理求物块P到达C点时速度的大小.
(2)P由D到达E点作平抛运动,由平抛运动下降的高度和水平位移大小结合求出物块P运动到D点时速度.P由B到达D点,运用动能定理求改变后物块P的质量.
解答 解:(1)6m的物体置于弹簧的顶端由静止释放,由机械能守恒得弹簧的弹性势能为:EP=6mgR
P由B到达C点,由动能定理有:W弹-mg$\overline{BC}$sin37°-μmgcos37°•$\overline{BC}$=$\frac{1}{2}m{v}_{C}^{2}$-0
由功能关系有:W弹=EP
得:vC=$\sqrt{2gR}$
(2)P由D到达E点作平抛运动,有:
R+Rcos37°=$\frac{1}{2}g{t}^{2}$
$\overline{EC}$-Rsin37°=vDt
解得:vD=$\sqrt{\frac{18}{5}gR}$
P由B到达D点,由动能定理有:
W弹-m′g$\overline{BC}$sin37°-μm′gcos37°•$\overline{BC}$-m′g(R+Rcos37°)=$\frac{1}{2}m′{v}_{D}^{2}$-0
解得:m′=$\frac{30}{43}$m
答:(1)若物块P的质量为m,物块P到达C点时速度的大小是$\sqrt{2gR}$:
(2)物块P运动到D点时速度的大小是$\sqrt{\frac{18}{5}gR}$,改变后物块P的质量是$\frac{30}{43}$m.
点评 本题要分析清楚物体的运动情况,抓住弹簧的弹性势能与形变量有关,对于两种情况,要抓住弹性势能相等.对动能定理的运用,要选择研究过程,分析哪些力对物体做功,进而确定合力的功或总功.

 通城学典默写能手系列答案
通城学典默写能手系列答案 如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动一段距离.在此过程中( )
如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动一段距离.在此过程中( )| A. | 外力F做的功等于A和B动能的增量 | |
| B. | B对A的摩擦力所做的功,等于A的动能增量 | |
| C. | A对B的摩擦力所做的功,等于B对A的摩擦力所做的功 | |
| D. | 外力F对B做的功等于B的动能的增量 |
| A. | 牛顿 | B. | 伽利略 | C. | 法拉第 | D. | 麦克斯韦 |
 如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )
如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )| A. | 在该过程中,物块的运动是加速的 | |
| B. | 在该过程中,人对物块做的功为$\frac{{m{v^2}{x^2}}}{{2({h^2}+{x^2})}}$ | |
| C. | 在该过程中,人对物块做的功为$\frac{1}{2}m{v^2}$ | |
| D. | 人前进x时,物块的运动速率为$\frac{vx}{{\sqrt{{x^2}+{h^2}}}}$ |
| A. | 卫星的速度大小为$\frac{{\sqrt{2gR}}}{2}$ | B. | 卫星的角速度大小$\sqrt{\frac{g}{8R}}$ | ||
| C. | 卫星的加速度大小为 $\frac{g}{2}$ | D. | 卫星的运动周期为2π$\sqrt{\frac{2R}{g}}$ |
 如图,在磁感应强度为B的匀强磁场中有一个粒子放射源O,某时刻在纸面内以相同的速率向各个方向发射了大量的电荷量为q、质量为m的带电粒子,经过时间t后这些粒子所在的位置第一次形成了一个半径最大且大小为R的圆,粒子仅受洛仑兹力,则下列说法正确的是( )
如图,在磁感应强度为B的匀强磁场中有一个粒子放射源O,某时刻在纸面内以相同的速率向各个方向发射了大量的电荷量为q、质量为m的带电粒子,经过时间t后这些粒子所在的位置第一次形成了一个半径最大且大小为R的圆,粒子仅受洛仑兹力,则下列说法正确的是( )| A. | 带电粒子发射的速率为$\frac{qBR}{m}$ | |
| B. | 带电粒子发射的速率为$\frac{qBR}{2m}$ | |
| C. | 带电粒子在磁场中做圆周运动的周期为t | |
| D. | 再经过$\frac{t}{2}$的时间,粒子所在位置形成的圆的半径为$\frac{\sqrt{2}}{2}$R |
 在“研究平抛物体的运动”的实验中,某同学在平抛运动轨迹上选取A、B两点,现测得A点的速度方向与水平方向的夹角为30°,B点的速度方向与水平方向的夹角为60°.从抛出点分別到A、B点的水平位移之比为1:3;从抛出点分别到A、B点的竖直位移之比为1:9.
在“研究平抛物体的运动”的实验中,某同学在平抛运动轨迹上选取A、B两点,现测得A点的速度方向与水平方向的夹角为30°,B点的速度方向与水平方向的夹角为60°.从抛出点分別到A、B点的水平位移之比为1:3;从抛出点分别到A、B点的竖直位移之比为1:9.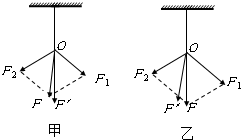 (1)在做“探究合力与分力关系”的实验时,橡皮条的一端固定在木板上,用两个弹簧秤把橡皮条的另一端拉到某一确定的O点,则下列说法中正确的是AB
(1)在做“探究合力与分力关系”的实验时,橡皮条的一端固定在木板上,用两个弹簧秤把橡皮条的另一端拉到某一确定的O点,则下列说法中正确的是AB