题目内容
1．
如图所示的装置中，木块B与水平桌面间的接触是光滑的，子弹A沿水平方向射入木块后留在木块内，将弹簧压缩到最短．现将子弹、木块和弹簧合在一起作为研究对象（系统），则此系统在从子弹开始射入到弹簧被压缩至最短的整个过程中（ ）| A． | 动量守恒，机械能守恒 | B． | 动量守恒，机械能不守恒 | ||
| C． | 动量不守恒，机械能守恒 | D． | 动量不守恒，机械能不守恒 |
分析 根据系统所受合外力是否为零，判断系统动量是否守恒，只有重力或只有弹力做功，系统机械能守恒；根据物体受力情况分析答题．
解答 解：此系统在从子弹开始射入到弹簧被压缩至最短的整个过程中水平方向受到墙壁对系统的向右的作用力，所以系统的动量不守恒；子弹在进入木块的过程中，子弹相对于木块有一定的位移，所以子弹与木块组成的系统有一定的动能损失，所以系统的机械能也不守恒．故D正确，ABC错误．
故选：D
点评 分析清楚物体运动过程、掌握系统动量守恒的条件、机械能守恒的条件是解题的关键，以及知道当系统只有动能和势能之间相互转化时，系统机械能守恒．分析清楚运动过程即可正确解题．
练习册系列答案
相关题目
11．
如图所示，光滑绝缘的水平面上M、N两点各放一带电荷量分别为+q和+2q的完全相同的刚性金属球A和B，给A和B以大小相等的初动能E0（此时初动量的大小均为p0），使其相向运动一段距离后发生弹性正碰，碰后返回M、N两点的动能分别为E1和E2，动量的大小分别为p1和p2，则（ ）
如图所示，光滑绝缘的水平面上M、N两点各放一带电荷量分别为+q和+2q的完全相同的刚性金属球A和B，给A和B以大小相等的初动能E0（此时初动量的大小均为p0），使其相向运动一段距离后发生弹性正碰，碰后返回M、N两点的动能分别为E1和E2，动量的大小分别为p1和p2，则（ ）| A． | E1=E2=E0，p1=p2=p0 | B． | E1=E2＞E0，p1=p2＞p0 | ||
| C． | 碰撞发生在MN连线的中点 | D． | 碰撞发生在MN连线中点的左侧 |
12．图示为一质点在0～4s内做直线运动的v-t图象．由图可得（ ）
| A． | 在1s～3s内，合力对质点不做功 | |
| B． | 在0～1s，合力对质点不做功 | |
| C． | 在0～1s和3s～4s内，合力对质点做的功相同 | |
| D． | 在0～4s内，合力对质点做的功为零 |
9．通过观测冥王星的卫星，可以推算出冥王星的质量．假设卫星绕冥王星做匀速圆周运动，除了引力常量外，至少还需要两个物理量才能计算出冥王星的质量．这两个物理量可以是（ ）
| A． | 卫星的质量和轨道半径 | B． | 卫星的速度和角速度 | ||
| C． | 卫星的质量和角速度 | D． | 卫星的运行周期和轨道半径 |
6．一质点在某段时间内做曲线运动，则在这段时间内（ ）
| A． | 速度一定在不断地改变，加速度可以不变 | |
| B． | 速度一定在不断地改变，加速度也一定在不断地改变 | |
| C． | 速度一定在不断地改变，加速度也可以在不断地改变 | |
| D． | 速度可以不变，加速度也一定在不断地改变 |
13．
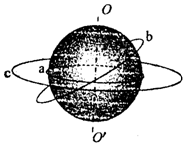如图所示，a为放在赤道上相对地球静止的物体，随地球自转做匀速圆周运动，b为沿地球表面附近做匀速圆周运动的人造卫星（轨道半径近似等于地球半径），c为地球的同步卫星，以下关于a、b、c的说法中正确的是（ ）
如图所示，a为放在赤道上相对地球静止的物体，随地球自转做匀速圆周运动，b为沿地球表面附近做匀速圆周运动的人造卫星（轨道半径近似等于地球半径），c为地球的同步卫星，以下关于a、b、c的说法中正确的是（ ）| A． | a、b、c的角速度大小关系为ωa=ωb＞ωc | |
| B． | a、b、c的向心加速度大小关系为ab＞ac＞aa | |
| C． | a、b、c的线速度大小关系为va=vb＞vc | |
| D． | a、b、c的周期关系为Ta=Tc＜Tb |
11．图甲为某一列沿x轴正向传播的简谐横波在t=1s时刻的波形图，图乙为参与波动的某一质点的振动图象，则下列说法正确的是（ ）
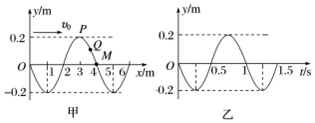
| A． | 该简谐横波的传播速度为4 m/s | |
| B． | 从此时刻起，经过2s，P质点运动了8m的路程 | |
| C． | 从此时刻起，P质点比Q质点先回到平衡位置 | |
| D． | 图乙可能是图甲x=4 m处质点的振动图象 |