题目内容
1.悬停在空中的直升飞机上坠落一物体,可视为做自由落体运动.从下落开始计时,重力加速度g取l0m/s2,则物体在第5s内的位移为( )| A. | 10m | B. | 45m | C. | 80m | D. | 125m |
分析 第5s内的位移等于前5s内位移减去前4s内位移,根据自由落体运动的位移时间公式求解.
解答 解:设运动的总时间为t,则第5s内的位移为:
x=$\frac{1}{2}$gt2-$\frac{1}{2}$g(t-1)2=$\frac{1}{2}$×10×52-$\frac{1}{2}$×10×42=45m
故选:B
点评 本题主要考查了自由落体运动的位移时间公式的直接应用,要知道各段时间内位移的关系,本题也可以用比例求解.

练习册系列答案
相关题目
16.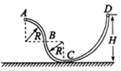 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )| A. | 若小球恰好能够到达水平管口A处,则H>2R | |
| B. | 若小球恰好能够到达水平管口A处,则H=2R | |
| C. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{1}{2}$R | |
| D. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{5}{2}$R |
13.某极地卫星(即运行轨道经过南北两极的卫星)的运行周期T=1.5h,某时刻该卫星恰好经过一赤道小岛上空.已知地球自转周期T0=24h,地球同步卫星轨道半径为r,引力常量为G,根据上述条件( )
| A. | 可以计算极地卫星绕地球运动的圆轨道半径 | |
| B. | 可以计算地球的质量 | |
| C. | 可以计算地球表面的重力加速度 | |
| D. | 可以断定,再经过12h极地卫星第二次到达该小岛上空 |
10.下列说法正确的是( )
| A. | 经典力学中物体的质量是可变的 | |
| B. | 经典力学中的时间和空间是独立于物体及其运动的 | |
| C. | 万有引力定律适用于强引力作用 | |
| D. | 物体的速度可以是任意数值 |
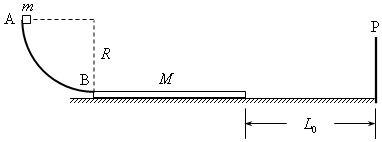
 如图所示,特种兵(视为质点)训练时,抓住一端固定的水平伸直的绳索,从平台边缘由静止开始下摆,当到达竖直状态时放开绳索,特种兵水平抛出,顺利越过距平台S=3.25m处的障碍物(竖直放置,厚度不计)后落入水中.已知特种兵质量m=70kg,平台到地面的高度H=8m,绳长l=1.25m,不计绳索质量和空气阻力,取重力加速度g=10m/s2.求:
如图所示,特种兵(视为质点)训练时,抓住一端固定的水平伸直的绳索,从平台边缘由静止开始下摆,当到达竖直状态时放开绳索,特种兵水平抛出,顺利越过距平台S=3.25m处的障碍物(竖直放置,厚度不计)后落入水中.已知特种兵质量m=70kg,平台到地面的高度H=8m,绳长l=1.25m,不计绳索质量和空气阻力,取重力加速度g=10m/s2.求: 皮带轮的大轮、小轮的半径不一样,它们的边缘有两个点A、B,如图所示.皮带轮正常运转不打滑时,A、B两点具有相同的线速度(填“线速度”或“角速度”),A点的向心加速度<B点的向心加速度(填“>”或“=”或“<”)
皮带轮的大轮、小轮的半径不一样,它们的边缘有两个点A、B,如图所示.皮带轮正常运转不打滑时,A、B两点具有相同的线速度(填“线速度”或“角速度”),A点的向心加速度<B点的向心加速度(填“>”或“=”或“<”)


