题目内容
8. 如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v1、v2沿水平方向抛出甲、乙两个相同的小球并分别落在M、N两点已知OM、ON与竖直方向的夹角均为30°,不考虑空气阻力,则下列结论正确的是( )
如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v1、v2沿水平方向抛出甲、乙两个相同的小球并分别落在M、N两点已知OM、ON与竖直方向的夹角均为30°,不考虑空气阻力,则下列结论正确的是( )| A. | 甲球比乙球先落到轨道上 | |
| B. | 甲、乙两球在下落过程中受到的冲量相同 | |
| C. | v1:v2=1:2 | |
| D. | v1:v2=1:3 |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据平抛运动水平位移和竖直位移的关系确定两小球初速度大小之比.
解答 解:A、由图且已知OM、ON与竖直方向的夹角均为30°,可知两个物体下落的高度是相等的,根据:h=$\frac{1}{2}g{t}^{2}$可知,甲乙两球下落到轨道的时间相等,故A错误;
B、甲乙两球下落到轨道的时间相等,则速度变化量△v=gt相同,动量的变化量:△P=m△v也相等,由动量定理可得甲、乙两球在下落过程中受到的冲量相同.故B正确;
CD、设圆形轨道的半径为R.则A、C的水平位移为 x1=R-Rsin30°=0.5R,x2=R+Rsin30°=1.5R,则x2=3x1;
由h=$\frac{1}{2}g{t}^{2}$,可知t相同,则由v=$\frac{x}{t}$可知,v2=3v1.故C错误,D正确;
故选:BD
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
18.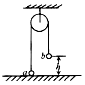 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )| A. | $\frac{m}{M+m}$h | B. | $\frac{M}{M+m}$h | C. | $\frac{2m}{M+m}$h | D. | $\frac{2M}{M+m}$h |
16.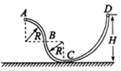 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )| A. | 若小球恰好能够到达水平管口A处,则H>2R | |
| B. | 若小球恰好能够到达水平管口A处,则H=2R | |
| C. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{1}{2}$R | |
| D. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{5}{2}$R |
3. 如图为氢原子的能级图,现有大量处于n=4激发态的氢原子向低能级跃迁,下列说法正确的是( )
如图为氢原子的能级图,现有大量处于n=4激发态的氢原子向低能级跃迁,下列说法正确的是( )
 如图为氢原子的能级图,现有大量处于n=4激发态的氢原子向低能级跃迁,下列说法正确的是( )
如图为氢原子的能级图,现有大量处于n=4激发态的氢原子向低能级跃迁,下列说法正确的是( )| A. | 氢原子由n=4跃迁到n=2产生的光照射逸出功为6.34eV的金属铂能发生光电效应 | |
| B. | 这些氢原子总共克辐射出三种不同频率的光 | |
| C. | 这些氢原子跃迁时辐射出光子能量的最大值为10.2eV | |
| D. | 氢原子由n=3跃迁到n=2能级时,其核外电子的动能增加,电势能减少 |
13.某极地卫星(即运行轨道经过南北两极的卫星)的运行周期T=1.5h,某时刻该卫星恰好经过一赤道小岛上空.已知地球自转周期T0=24h,地球同步卫星轨道半径为r,引力常量为G,根据上述条件( )
| A. | 可以计算极地卫星绕地球运动的圆轨道半径 | |
| B. | 可以计算地球的质量 | |
| C. | 可以计算地球表面的重力加速度 | |
| D. | 可以断定,再经过12h极地卫星第二次到达该小岛上空 |
20.关于力和运动,下列说法中正确的是( )
| A. | 如果物体运动,它一定受到力的作用 | |
| B. | 力是使物体做变速运动的原因 | |
| C. | 力是使物体产生加速度的原因 | |
| D. | 力只能改变速度的大小 |
 如图,设想光滑水平面上有两同样大小的小球,质量为m1的小球A以v1速度向右作匀速直线运动,与质量为m2的静止小球B发生碰撞,碰后小球A速度变为v1′,小球B速度变为v2′,方向均向右,若规定向右为正方向.试分析:
如图,设想光滑水平面上有两同样大小的小球,质量为m1的小球A以v1速度向右作匀速直线运动,与质量为m2的静止小球B发生碰撞,碰后小球A速度变为v1′,小球B速度变为v2′,方向均向右,若规定向右为正方向.试分析: 某同学设计如图(甲)所示的实验装置,通过半径相同的A、B两球的碰撞来探究碰撞时动量变化的规律,图中PQ是斜槽,QR为水平槽.实验时先使A球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.重复上述操作10次,得到10个落点痕迹,再把B球放在水平槽上靠近末端的地方,让A球仍从位置G由静止开始滚下,和B球碰撞后,A,B球分别在记录纸上留下各自的落点痕迹,重复这种操作10次.图中O点是水平槽末端R在记录纸上的垂直投影点,B球落点痕迹如图(乙)所示,其中米尺水平放置,且平行于G、R、O所在的平面,米尺的零点与O点对齐.
某同学设计如图(甲)所示的实验装置,通过半径相同的A、B两球的碰撞来探究碰撞时动量变化的规律,图中PQ是斜槽,QR为水平槽.实验时先使A球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.重复上述操作10次,得到10个落点痕迹,再把B球放在水平槽上靠近末端的地方,让A球仍从位置G由静止开始滚下,和B球碰撞后,A,B球分别在记录纸上留下各自的落点痕迹,重复这种操作10次.图中O点是水平槽末端R在记录纸上的垂直投影点,B球落点痕迹如图(乙)所示,其中米尺水平放置,且平行于G、R、O所在的平面,米尺的零点与O点对齐.