题目内容
14. 如图所示,水平虚线L1、L2之间是匀强磁场,磁场区竖直宽度为h,磁场方向水平向里.竖直平面内有一等腰梯形导线框,底边水平,其上下边长之比为5:1,高为2h.现使线框AB边在磁场边界L1的上方h高处由静止自由下落,当AB边刚进入磁场时加速度恰好为0,在DC边刚要进入磁场前的一小段时间内,线框做匀速运动.重力加速度为g.
如图所示,水平虚线L1、L2之间是匀强磁场,磁场区竖直宽度为h,磁场方向水平向里.竖直平面内有一等腰梯形导线框,底边水平,其上下边长之比为5:1,高为2h.现使线框AB边在磁场边界L1的上方h高处由静止自由下落,当AB边刚进入磁场时加速度恰好为0,在DC边刚要进入磁场前的一小段时间内,线框做匀速运动.重力加速度为g.(1)如果已知磁感应强度为B,导线框电阻为R,AB长为l,求线框的质量;
(2)求在DC边进入磁场前,线框做匀速运动时的速度大小与AB边刚进入磁场时的速度大小之比;
(3)求DC边刚进入磁场时,线框加速度的大小.
分析 (1)由机械能守恒求出AB刚进入磁场时的速度,根据AB刚进入磁场时加速度恰好为0,由平衡条件求出线框的质量.
(2)在DC边刚进入磁场前的一段时间内,线框做匀速运动,此时线框有效切割长度为2l,由平衡条件得到重力与安培力的关系式,将两个重力与安培力的关系式进行对比,求出DC边刚进入磁场前线框匀速运动时的速度.然后求出速度之比.
(3)DC边刚进入磁场瞬间,线框有效切割的长度为3l,推导出安培力表达式,由牛顿第二定律求出加速度.
解答 解:(1)设AB边刚进入磁场时速度为v0,线框质量为m、电阻为R,
设AB=l,已知AB与CD之比为:5:1,则CD=5l,
从线框开始运动到AB边进入磁场过程,由机械能守恒定律得:mgh=$\frac{1}{2}$mv02,
AB刚进入磁场时加速度为零,则线框所受合力为零,
由平衡条件得:$\frac{{B}^{2}{l}^{2}{v}_{0}}{R}$=mg,解得:m=$\frac{{B}^{2}{l}^{2}\sqrt{2gh}}{gR}$,v0=$\frac{mgR}{{B}^{2}{l}^{2}}$;
(2)DC边刚进入磁场前匀速运动时速度为v1,线框切割磁感应线的有效长度 为2l,感应电动势:E=$\frac{△Φ}{△t}$=$\frac{B△S}{△t}$=$\frac{B({L}_{上}-{L}_{下}){v}_{1}△t}{△t}$=2Blv1,
为2l,感应电动势:E=$\frac{△Φ}{△t}$=$\frac{B△S}{△t}$=$\frac{B({L}_{上}-{L}_{下}){v}_{1}△t}{△t}$=2Blv1,
框匀速运动时,处于平衡状态,由平衡条件得:$\frac{{B}^{2}(2l)^{2}{v}_{1}}{R}$=mg,
解得:v1=$\frac{mgR}{4{B}^{2}{l}^{2}}$,则:速度之比:v1:v0=1:4;
(3)CD刚进入磁场瞬间,线框切割磁感应线的有效长度为3l,
感应电动势:E感′=B•3l•v1 ,安培力:F1=BI1•3l=$\frac{{B}^{2}(3l)^{2}{v}_{1}}{R}$=$\frac{9}{4}$mg,
由牛顿第二定律得:F1-mg=ma,解得:a=$\frac{5}{4}$g;
答:(1)如果已知磁感应强度为B,导线框电阻为R,AB长为l,线框的质量为=$\frac{{B}^{2}{l}^{2}\sqrt{2gh}}{gR}$;
(2)在DC边进入磁场前,线框做匀速运动时的速度大小与AB边刚进入磁场时的速度大小之比为1:4;
(3)求DC边刚进入磁场时,线框加速度的大小为$\frac{5}{4}$g.
点评 本题要研究物体多个状态,再找它们的关系,关键要写出线框有效的切割长度,即与速度方向垂直的导体等效长度.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | α粒子散射实验是估算原子核半径最简单的方法之一 | |
| B. | 光子像其他粒子一样,不但具有能量,也具有质量 | |
| C. | 玻尔理论认为原子的能量是连续的,电子的轨道半径是不连续的 | |
| D. | 光照到某金属上不能发生光电效应,是因为该光波长太短 |

| A. | 线框中感应电流i随时间t的变化关系是i=$\frac{{\sqrt{2}B{L^2}ω}}{R}$cos(ωt+$\frac{π}{4}$) | |
| B. | 线框中感应电流i随时间t的变化关系是i=$\frac{{B{L^2}ω}}{R}$•cosωt | |
| C. | 在t=0时刻,线框中的感应电流最大 | |
| D. | 从0~$\frac{π}{2ω}$时间内,感应电流方向改变1次 |
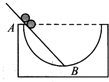 如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )
如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )| A. | a、b两球有可能同时到达B点 | |
| B. | b球打在B点的速度方向可能垂直于该点的切线方向 | |
| C. | 若a球到达B点的时间是b球的两倍,则木板与水平方向的夹角是60° | |
| D. | 撤去木板,如果v0=$\sqrt{gR}$时,则可判断b球落点位于凹槽最低点的右侧 |
 质量相同的甲、乙两物体放在相同的光滑水平地面上,分别在水平力F1、F2的作用下从同一地点,沿同一方向,同时运动,其v-t图象如图所示,下列判断正确的是( )
质量相同的甲、乙两物体放在相同的光滑水平地面上,分别在水平力F1、F2的作用下从同一地点,沿同一方向,同时运动,其v-t图象如图所示,下列判断正确的是( )| A. | 在0~2s内,F1越来越大 | |
| B. | 4s末甲、乙两物体动能相同,由此可知F1=F2 | |
| C. | 4~6s内两者逐渐靠近 | |
| D. | 0~6s内两者在前进方向上的最大距离为4m |
| A. | 原子核发生一次β衰变,该原子外层就失去一个电子 | |
| B. | 普朗克在1900年将“能量子”引入物理学,破除“能量连续变化”的传统观念,成为近代物理学思想的基石之一 | |
| C. | 美国物理学家密立根,测量金属的遏止电压UC与入射光的频率ν,由此算出普朗克常量h,并与普朗克根据黑体辐射得出的h相比较,以此检验了爱因斯坦光电效应的正确性 | |
| D. | 英国物理学家汤姆孙根据阴极射线在电场和磁场中的偏转情况断定,它的本质是带负电的粒子流并求出了这种粒子的比荷,从而发现了电子 | |
| E. | 所有的核反应都遵循核电荷数守恒,反应前后核的总质量也保持不变 |
 如图,质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=20g的子弹以水平速度v0=20m/s射入物块,在很短的时间内以水平速度v1=10m/s穿出木块.重力加速度g取10m/s2,求:
如图,质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=20g的子弹以水平速度v0=20m/s射入物块,在很短的时间内以水平速度v1=10m/s穿出木块.重力加速度g取10m/s2,求:
 在甘肃省“月牙泉、鸣沙山”风景名胜区里有一种滑沙运动.简化为如图所示模型:某人坐在滑板上从斜坡的高出A点由静止开始滑下,滑到斜坡底端B点后,压水平的滑到再滑行一段距离到C点停下来,若人和滑板的总质量M=60kg(其中滑板质量m=3kg),滑板与斜坡滑到和水平滑到间的动摩擦因数均为μ=0.50,斜坡的倾角θ=65°(sin65°=0.91,cos65°=0.42),斜坡与水平滑到间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2,求:
在甘肃省“月牙泉、鸣沙山”风景名胜区里有一种滑沙运动.简化为如图所示模型:某人坐在滑板上从斜坡的高出A点由静止开始滑下,滑到斜坡底端B点后,压水平的滑到再滑行一段距离到C点停下来,若人和滑板的总质量M=60kg(其中滑板质量m=3kg),滑板与斜坡滑到和水平滑到间的动摩擦因数均为μ=0.50,斜坡的倾角θ=65°(sin65°=0.91,cos65°=0.42),斜坡与水平滑到间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2,求: