题目内容
12.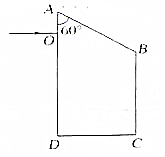 如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:
如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:①临界角及光线第一次射出棱镜时,出射光线的方向.
②第一次的出射点到D点的距离.
分析 ①根据sinC=$\frac{1}{n}$,求出临界角的大小,判断知道光线在AB面和BC面能否发生全反射,从而作出光路图,根据几何关系,结合折射定律求出出射光线的方向.
②根据几何关系,求出第一次的出射点距D点的距离.
解答  解:①设全反射的临界角为C,则有:sin C=$\frac{1}{n}$
解:①设全反射的临界角为C,则有:sin C=$\frac{1}{n}$
代入数据得:C=45°
光路图如图所示,由几何关系可知光线在AB边和BC边的入射角均为60°,均发生了全反射
设光线在CD边的入射角为i、折射角为r,由几何关系得 i=30°,小于临界角,则光线第一次射出棱镜是在CD边
由折射定律得:n=$\frac{sinr}{sini}$
代入数据得:r=45°
故光线第一次从CD边射出棱镜时与CD边成45°角斜向左下方.
②由几何知识可知:AE=2OA=3cm,BF=EB=AB-AE=6cm-3cm=3cm
FC=BC-BF=6cm-3cm=3cm
出射点G距D点的距离为:
GC=DC-FCtan30°=OAtan60°-FCtan30°=1.5×$\sqrt{3}$-3×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{2}$cm
答:①临界角为45°,光线第一次从CD边射出棱镜时与CD边成45°角斜向左下方.
②第一次的出射点到D点的距离是$\frac{\sqrt{3}}{2}$cm.
点评 解决本题的关键掌握全发射的条件,以及折射定律,作出光路图,结合几何关系进行求解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
17.下列四种现象不属于光的衍射现象的是( )
| A. | 太阳光照射下,架在空中的电线在地面上不会留下影子 | |
| B. | 不透光的圆片后面的阴影中心出现一个泊松亮斑 | |
| C. | 用点光源照射小圆孔,后面屏上会出现明暗相间的圆环 | |
| D. | 通过游标卡尺两卡脚间的狭缝观察发光的日光灯管,会看到平行的彩色条纹 |
7.将两个可视为质点的小球放在桌面上,两小球之间的万有引力大小为F,若两小球的质量均增加到原来的3倍,同时它们之间的距离亦增加到原来的3倍,则两小球间的万有引力大小将为( )
| A. | $\frac{F}{3}$ | B. | F | C. | 6F | D. | 9F |
4. 如图所示,竖直面内有一个固定圆环,MN是它在竖直方向上的直径.两根光滑滑轨MP、QN的端点都在圆周上,MP>QN.将两个完全相同的小球a、b分别从M、Q点无初速释放,在它们各自沿MP、QN运动到圆周上的过程中,下列说法中正确的是( )
如图所示,竖直面内有一个固定圆环,MN是它在竖直方向上的直径.两根光滑滑轨MP、QN的端点都在圆周上,MP>QN.将两个完全相同的小球a、b分别从M、Q点无初速释放,在它们各自沿MP、QN运动到圆周上的过程中,下列说法中正确的是( )
 如图所示,竖直面内有一个固定圆环,MN是它在竖直方向上的直径.两根光滑滑轨MP、QN的端点都在圆周上,MP>QN.将两个完全相同的小球a、b分别从M、Q点无初速释放,在它们各自沿MP、QN运动到圆周上的过程中,下列说法中正确的是( )
如图所示,竖直面内有一个固定圆环,MN是它在竖直方向上的直径.两根光滑滑轨MP、QN的端点都在圆周上,MP>QN.将两个完全相同的小球a、b分别从M、Q点无初速释放,在它们各自沿MP、QN运动到圆周上的过程中,下列说法中正确的是( )| A. | 两球的动量变化大小相同 | B. | 重力对两球的冲量大小相同 | ||
| C. | 合力对a球的冲量较大 | D. | 弹力对a球的冲量较大 |
1.如图所示,一束光由空气射入某种介质,该介质的折射率等于( )


| A. | $\frac{sin50°}{sin55°}$ | B. | $\frac{sin55°}{sin50°}$ | C. | $\frac{sin40°}{sin35°}$ | D. | $\frac{sin35°}{sin40°}$ |
12. 现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )
现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )
 现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )
现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )| A. | 可以确定该粒子一定带负电 | B. | 可以测得该粒子的带电量 | ||
| C. | 不能测得该粒子的比荷 | D. | 可以测得该粒子的离开磁场的速度 |
 如图所示,在方向竖直向上、大小为E=1×106V/m的匀强电场中,固定一个穿有A、B两个小球(均视为质点)的光滑绝缘圆环,圆环在竖直平面内,圆心为O、半径为R=0.2m.A、B用一根绝缘轻杆相连,A带的电荷量为q=+7×10-7C,B不带电,质量分别为mA=0.01kg、mB=0.08kg.将两小球从圆环上的图示位置(A与圆心O等高,B在圆心O的正下方)由静止释放,两小球开始沿逆时针方向转动.重力加速度大小为g=10m/s2.
如图所示,在方向竖直向上、大小为E=1×106V/m的匀强电场中,固定一个穿有A、B两个小球(均视为质点)的光滑绝缘圆环,圆环在竖直平面内,圆心为O、半径为R=0.2m.A、B用一根绝缘轻杆相连,A带的电荷量为q=+7×10-7C,B不带电,质量分别为mA=0.01kg、mB=0.08kg.将两小球从圆环上的图示位置(A与圆心O等高,B在圆心O的正下方)由静止释放,两小球开始沿逆时针方向转动.重力加速度大小为g=10m/s2.