题目内容
4. 如图所示,竖直面内有一个固定圆环,MN是它在竖直方向上的直径.两根光滑滑轨MP、QN的端点都在圆周上,MP>QN.将两个完全相同的小球a、b分别从M、Q点无初速释放,在它们各自沿MP、QN运动到圆周上的过程中,下列说法中正确的是( )
如图所示,竖直面内有一个固定圆环,MN是它在竖直方向上的直径.两根光滑滑轨MP、QN的端点都在圆周上,MP>QN.将两个完全相同的小球a、b分别从M、Q点无初速释放,在它们各自沿MP、QN运动到圆周上的过程中,下列说法中正确的是( )| A. | 两球的动量变化大小相同 | B. | 重力对两球的冲量大小相同 | ||
| C. | 合力对a球的冲量较大 | D. | 弹力对a球的冲量较大 |
分析 先受力分析后根据牛顿第二定律计算出滑环沿任意一根杆滑动的加速度,然后根据位移时间关系公式计算出时间,然后结合冲量的定义以及.
解答 解:对小球,受重力和支持力,将重力沿轨道的方向和垂直杆的方向正交分解,根据牛顿第二定律得小滑环做初速为零的匀加速直线运动的加速度为
a=gsinθ(θ为杆与水平方向的夹角)
由图中的直角三角形可知,小滑环的位移S=2Rsinθ
所以$t=\sqrt{\frac{2S}{a}}=\sqrt{\frac{2×2Rsinθ}{gsinθ}}=\sqrt{\frac{4R}{g}}$,t与θ无关,即t1=t2
A、C、小球受到的合外力等于重力沿轨道方向的分力,即:mgsinθ,所以合外力的冲量大小为:mgsinθ•t.由图可知MP与水平方向之间的夹角大,所以沿MP运动的a球受到的合外力的冲量大;沿MP运动的a球受到的合外力的冲量大,由动量定理可知,a球的动量变化大.故A错误,C正确;
B、重力的冲量为mgt,由于运动的时间相等,所以重力的冲量大小相等.故B正确;
D、弹力的冲量:mgcosθ•t,由图可知MP与水平方向之间的夹角大,所以a球的弹力的冲量小.故D错误.
故选:BC
点评 该题也可以根据“等时圆”的适用条件构造出“等时圆”,作出图象,根据位移之间的关系即可判断运动时间,难度适中.

练习册系列答案
相关题目
9.一辆小汽车,分别以相同的速率经过半径相同的拱形路面的最高点和凹形路面的最低点.车对拱形路面顶部的压力大小为N1,车对凹形路面底部的压力大小为N2,则N1与 N2的大小关系是( )


| A. | N1>N2 | B. | N1=N2 | C. | N1<N2 | D. | 无法判断 |
15.质量为m的物体在水平恒力F的作用下,由静止开始在光滑水平地面上运动距离为x1 时速度大小为v,此过程的动能增量为△Ek1;再运动距离x2时速度大小为2v,此过程的动能增量为△Ek2.下列说法正确的是 )
| A. | △Ek1=△Ek2 | B. | △Ek1<△Ek2 | C. | x2=3x1 | D. | x2<3x1 |
9.已知入射角i=60°,b光在三棱镜中的折射角r=45°,该三棱镜对b光的折射率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
16.在力学范围内,国际单位制规定了三个基本单位量,它们是( )
| A. | 长度、质量、力 | B. | 质量、时间、力 | C. | 时间、位移、力 | D. | 长度、质量、时间 |
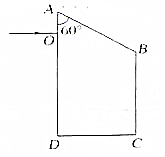 如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:
如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求: 某同学“验证动量守恒定律”的装置如图所示,滑块A、B上方固定遮光条.C、D为光电门.
某同学“验证动量守恒定律”的装置如图所示,滑块A、B上方固定遮光条.C、D为光电门.
