题目内容
12. 现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )
现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )| A. | 可以确定该粒子一定带负电 | B. | 可以测得该粒子的带电量 | ||
| C. | 不能测得该粒子的比荷 | D. | 可以测得该粒子的离开磁场的速度 |
分析 抓住粒子在电场中加速,得出电场力的方向,从而确定粒子的电性.根据动能定理和粒子在磁场中运动的半径公式得出半径r的表达式,从而分析判断.
解答 解:A、粒子在电场中加速,可知粒子所受电场力方向与电场强度方向相同,可知粒子带正电,故A错误.
B、根据动能定理得,qU=$\frac{1}{2}m{v}^{2}$,解得粒子进入磁场的速度v=$\sqrt{\frac{2qU}{m}}$,根据r=$\frac{mv}{qB}$=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$,已知B和U,不能求出粒子的带电量和粒子的比荷,故B错误,C正确.
D、根据v=$\sqrt{\frac{2qU}{m}}$知,由于比荷未知,无法求出粒子离开磁场的速度,故D错误.
故选:C.
点评 解决本题的关键知道粒子在电场中加速,在磁场中做匀速圆周运动,结合动能定理、牛顿运动定律进行求解,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列叙述正确的是( )
| A. | 力、长度和时间是力学中三个基本物理量,它们的单位牛顿、米和秒都是基本单位 | |
| B. | 蹦极运动员离开蹦床过程中处于失重状态 | |
| C. | 利用霍尔元件能够把电压这个电学量转换为磁感应强度这个磁学量的特性,可以制出测磁感应强度大小的仪器 | |
| D. | 探究加速度与质量、合力关系实验采用的是等效代替的方法 |
1. 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )| A. | b的伸长量为L | B. | b的伸长量为$\frac{{k}_{2}L}{{k}_{1}}$ | ||
| C. | 小球质量为$\frac{{k}_{1}L}{g}$ | D. | 小球质量为$\frac{{k}_{2}L}{g}$ |
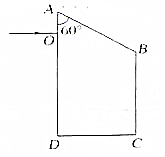 如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:
如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:





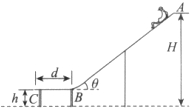 水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:
水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:
