题目内容
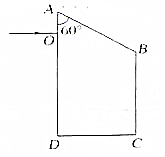
1.如图所示,一束光由空气射入某种介质,该介质的折射率等于( )
| A. | $\frac{sin50°}{sin55°}$ | B. | $\frac{sin55°}{sin50°}$ | C. | $\frac{sin40°}{sin35°}$ | D. | $\frac{sin35°}{sin40°}$ |
分析 由图确定出入射角和折射角,再根据光的折射定律求出介质的折射率大小.
解答 解:由图知,入射角为 i=90°-50°=40°
折射角为 r=90°-55°=35°
根据折射定律得:该介质的折射率 n=$\frac{sini}{sinr}$=$\frac{sin40°}{sin35°}$.故C正确,A、B、D错误.
故选:C
点评 解决本题的关键掌握光的折射定律,并能灵活运用.要注意入射角和折射角都是与法线的夹角,不是与界面的夹角.

练习册系列答案
相关题目
6.下列有关原子结构和原子核的认识,其中正确的是( )
| A. | 氢原子辐射光子后,其绕核运动的电子动能增大 | |
| B. | γ射线是高速运动的电子流 | |
| C. | 太阳辐射能量的主要来源是太阳中发生的重核裂变 | |
| D. | ${\;}_{83}^{210}Bi$的半衰期是5天,100克${\;}_{83}^{210}Bi$经过10天后还剩下50克 |
9.已知入射角i=60°,b光在三棱镜中的折射角r=45°,该三棱镜对b光的折射率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
16.在力学范围内,国际单位制规定了三个基本单位量,它们是( )
| A. | 长度、质量、力 | B. | 质量、时间、力 | C. | 时间、位移、力 | D. | 长度、质量、时间 |
1. 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )| A. | b的伸长量为L | B. | b的伸长量为$\frac{{k}_{2}L}{{k}_{1}}$ | ||
| C. | 小球质量为$\frac{{k}_{1}L}{g}$ | D. | 小球质量为$\frac{{k}_{2}L}{g}$ |
 如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求:
如图所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD射入.已知棱镜的折射率n=$\sqrt{2}$,AB=BC=6cm,OA=1.5cm,∠OAB=60°,求: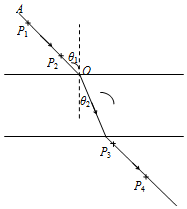 某同学利用“插针法”测定玻璃的折射率,所用的玻璃砖两面平行.正确操作后,作出的光路图及测出的相关角度如图所示.
某同学利用“插针法”测定玻璃的折射率,所用的玻璃砖两面平行.正确操作后,作出的光路图及测出的相关角度如图所示.




