题目内容
11. 如图所示,在匀强电场中,有A、B两点,它们间距为4cm,两点的连线与场强方向成60°角.将一个电量为-5×10-5C的电荷由A移到B,其电势能增加了0.2J.则:
如图所示,在匀强电场中,有A、B两点,它们间距为4cm,两点的连线与场强方向成60°角.将一个电量为-5×10-5C的电荷由A移到B,其电势能增加了0.2J.则:(1)在此过程中,电场力对该电荷做了多少功?
(2)A.B两点的电势差UAB为多少?
(3)匀强电场的场强为多大?
分析 (1)根据电势差的变化得出电场力做功;
(2)结合电场力做功与电势差的关系求出A、B两点的电势差.
(3)根据匀强电场的电场强度公式求出场强的大小.
解答 解:(1)根据电场力做功与电势能的关系可知,电场力所做的功:
W=-EP=-0.2J
(2)根据电场力做功的公式为:W=qU
可知:U=$\frac{W}{q}$=$\frac{-0.2}{-5×1{0}^{-5}}$=4000V
(3)AB沿电场线方向移动的距离为:D=4×cos60°=2cm=0.02m
有:E=$\frac{U}{d}$=$\frac{4000}{0.02}$=2.0×106V/m
答:(1)电场力对该电荷做了功-0.2J;
(2)A、B两点的电势差UAB为4000V;
(2)匀强电场的场强的大小为2.0×106V/m.
点评 解决本题的关键知道电场力做功等于电势差的减小量,掌握电场力做功与电势差的关系.注意运用W=qU计算时,功的正负、q的正负都要代入计算,以及在E=$\frac{U}{d}$中,d表示沿电场线方向上的距离.

练习册系列答案
相关题目
1.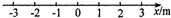 如图所示,在坐标轴正、负半轴上有两种不同的介质,原点处有一波源,波源起振后,波向左、右两介质中传播,P、Q是坐标分别为xP=-2m、xQ=2m处的两质点.关于P、Q两质点的振动情况,下列说法正确的是( )
如图所示,在坐标轴正、负半轴上有两种不同的介质,原点处有一波源,波源起振后,波向左、右两介质中传播,P、Q是坐标分别为xP=-2m、xQ=2m处的两质点.关于P、Q两质点的振动情况,下列说法正确的是( )
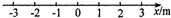 如图所示,在坐标轴正、负半轴上有两种不同的介质,原点处有一波源,波源起振后,波向左、右两介质中传播,P、Q是坐标分别为xP=-2m、xQ=2m处的两质点.关于P、Q两质点的振动情况,下列说法正确的是( )
如图所示,在坐标轴正、负半轴上有两种不同的介质,原点处有一波源,波源起振后,波向左、右两介质中传播,P、Q是坐标分别为xP=-2m、xQ=2m处的两质点.关于P、Q两质点的振动情况,下列说法正确的是( )| A. | 两质点一定同时起振 | |
| B. | 两质点的振动频率一定相同 | |
| C. | P质点到达波峰时,Q质点也一定到达波峰 | |
| D. | 两质点的振动方向不一定相同 | |
| E. | P、Q起振后,两质点分别连续五次出现波峰的时间间隔相同 |
2. 如图所示,A、B、C三球的质量均为m,轻质弹簧一段固定在斜面顶端,另一端与A球相连,倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,下列说法正确的是( )
如图所示,A、B、C三球的质量均为m,轻质弹簧一段固定在斜面顶端,另一端与A球相连,倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,下列说法正确的是( )
 如图所示,A、B、C三球的质量均为m,轻质弹簧一段固定在斜面顶端,另一端与A球相连,倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,下列说法正确的是( )
如图所示,A、B、C三球的质量均为m,轻质弹簧一段固定在斜面顶端,另一端与A球相连,倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,下列说法正确的是( )| A. | B球的受力情况未变,加速度为零 | |
| B. | A、B两球的加速度均沿斜面向上,大小均为gsinθ | |
| C. | A、B之间杆的拉力大小为1.5mgsinθ | |
| D. | C球的加速度沿斜面向下,大小为2gsinθ |
19. 沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )
沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )
 沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )
沿固定斜面下滑的物体受到与斜面平行向上的拉力F的作用,其下滑的速度-时间图线如图所示.已知物体与斜面之间的动摩擦因数为常数,在0-5s,5-10s,10-15s内F的大小分别为F1、F2和F3,则( )| A. | F1>F2 | B. | F2<F3 | C. | F1>F3 | D. | F1=F3 |
3. 如图所示,在光滑水平面上,用弹簧水平连接一斜面体,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动,然后人沿斜面加速上升,则( )
如图所示,在光滑水平面上,用弹簧水平连接一斜面体,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动,然后人沿斜面加速上升,则( )
 如图所示,在光滑水平面上,用弹簧水平连接一斜面体,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动,然后人沿斜面加速上升,则( )
如图所示,在光滑水平面上,用弹簧水平连接一斜面体,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动,然后人沿斜面加速上升,则( )| A. | 系统静止时弹簧处于压缩状态 | |
| B. | 系统静止时斜面体共受到4个力作用 | |
| C. | 人加速时弹簧伸长 | |
| D. | 人加速时斜面体对地面的压力变大 |
20.关于匀强电场中场强和电势差的关系,正确的是( )
| A. | 电场强度越大,则任意两点间的电势差不一定越大 | |
| B. | 任意两点间的电势差等于场强和这两点间距离的乘积 | |
| C. | 沿着电场线方向,任何相同距离上的电势降低必定相等 | |
| D. | 场强与电势处处相同 |
 如图所示,一块长木板B置于光滑的水平地面上,其质量为2kg,另有一个质量为0.8kg的小滑块A置于木板的一端,已知A与B之间的动摩擦因数为0.1,可以认为A、B之间的最大静摩擦力数值上等于它们之间的滑动摩擦力,木板在放置A的一端受到一个恒定的水平力F=5.6 N作用后,由静止开始滑动,如果木板足够长,那么当F作用在木板上1s后,求:
如图所示,一块长木板B置于光滑的水平地面上,其质量为2kg,另有一个质量为0.8kg的小滑块A置于木板的一端,已知A与B之间的动摩擦因数为0.1,可以认为A、B之间的最大静摩擦力数值上等于它们之间的滑动摩擦力,木板在放置A的一端受到一个恒定的水平力F=5.6 N作用后,由静止开始滑动,如果木板足够长,那么当F作用在木板上1s后,求: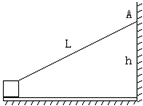 如图,厚度不计的长木板放在水平面上,并且右端紧靠竖直墙壁,木板与地面之间摩擦系数μ1=0.25,木板质量M=0.4kg,板上有一质量为m=0.3kg的小物体,与木板间摩擦系数μ2=$\frac{1}{3}$,将小物体用长为L=1m细绳系在墙上A点,A点高度h=0.6m,用水平力F=6.4N拉木板,使其从静止开始运动(此时细线是张紧的),问经多长时间小物体离开木板右端.
如图,厚度不计的长木板放在水平面上,并且右端紧靠竖直墙壁,木板与地面之间摩擦系数μ1=0.25,木板质量M=0.4kg,板上有一质量为m=0.3kg的小物体,与木板间摩擦系数μ2=$\frac{1}{3}$,将小物体用长为L=1m细绳系在墙上A点,A点高度h=0.6m,用水平力F=6.4N拉木板,使其从静止开始运动(此时细线是张紧的),问经多长时间小物体离开木板右端.