题目内容
2.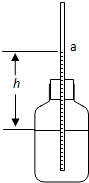 如图,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内水面有一定的高度差.已知地面附近高度每升高12m,大气压降低1mmHg;水银的密度为13.6×103kg/m3.
如图,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内水面有一定的高度差.已知地面附近高度每升高12m,大气压降低1mmHg;水银的密度为13.6×103kg/m3.将玻璃瓶放置在地面上,记录管内水面a的位置,再将玻璃瓶放到离地8m的三楼平台上,则玻璃管内水面a将上升(选填“上升”、“不动”或“下降”)9.1mm;(设温度保持不变;不计水面升降引起的瓶内空气体积的变化);用此装置可用来测量高度的变化:先将装置放在温度为27℃、大气压为750mmHg的A处,测得水柱的高度h=204mm.然后将装置缓慢地移到另一高度的B处,待稳定后发现水柱升高了40.8mm,已知B处比A处的温度高1℃,则AB间高度差为5.4m.该测量仪器选择瓶内装水而不装水银的主要原因是水的密度比水银小,同样的压强变化时高度变化明显.
分析 根据毛细管中高度差产生的压强加上大气压等于瓶中气体的压强列式计算;
先根据毛细管中高度差产生的压强加上大气压等于瓶中气体的压强列式计算出瓶内气压,然后根据理想气体状态方程列式求解出到达B处后的瓶内压强,最后得到B处的大气压强,并计算高度差.
水银密度是水的13.6倍,故同样的压强差,用水时高度差是用水银时高度差的13.6倍,故用水高度差大,现象明显;
解答 解:在地面附近高度每升高12m,大气压降低1mmHg,
所以玻璃瓶放到离地8m的三楼平台上时,大气压降低了$\frac{2}{3}$mmHg,毛细管中水面上升$\frac{2}{3}$mm×13.6=9mm;
大气压为750mmHg,在A处时,瓶内气体压强为:${P}_{1}=750mmHg+\frac{204}{13.6}mmHg$=765mmHg;
根据理想气体状态方程,有$\frac{{P}_{1}{V}_{1}}{{T}_{1}}=\frac{{P}_{2}{V}_{2}}{{T}_{2}}$,代入数据得到:$\frac{765×V}{300}=\frac{{P}_{2}V}{301}$,解得P2=767.55mmHg;
故B处大气压为${P}_{B}={P}_{2}-{P}_{h}=767.55mmhg-\frac{(204+40.8)mmHg}{13.6}$=749.55mmHg;
故A、B间的高度差为:△h=(750-749.55)×12=5.4m;
水银密度是水的13.6倍,故同样的压强差,用水时高度差是用水银时高度差的13.6倍,故用水高度差大,现象明显;
故答案为:上升;9.1;5.4;水的密度比水银小,同样的压强变化时高度变化明显.
点评 本题关键对高处瓶内水平面的液柱受力分析得到大气压强和瓶内气压的关系式,然后结合理想气体状态方程列式求解.

 如图所示为皮带传动装置,皮带轮的圆心分别为O、O′,A、C为皮带轮边缘上的点,B为A、O连线上的中点,RC=$\frac{1}{2}$RA,当皮带轮匀速转动时,皮带与皮带轮之间不打滑,求A、B、C三点的角速度之比、加速度之比分别为( )
如图所示为皮带传动装置,皮带轮的圆心分别为O、O′,A、C为皮带轮边缘上的点,B为A、O连线上的中点,RC=$\frac{1}{2}$RA,当皮带轮匀速转动时,皮带与皮带轮之间不打滑,求A、B、C三点的角速度之比、加速度之比分别为( )| A. | 1:1:2和2:1:4 | B. | 2:2:3和2:1:2 | C. | 1:1:2和1:2:1 | D. | 2:2:3和1:2:1 |
 磁场中某处的磁感线分布如图所示,下列说法正确的是( )
磁场中某处的磁感线分布如图所示,下列说法正确的是( )| A. | 磁感应强度Ba>Bb | |
| B. | 同一通电导线在b处所受的磁场力可能比在a处小 | |
| C. | 通电导线在b处所受磁场力的方向可能与b处磁感线的方向相同 | |
| D. | 若在a处的通电导线平行磁感线放置,则所受磁场力最大 |
| A. | 两星间的万有引力不变 | B. | 白矮星的轨道半径不变 | ||
| C. | 类日伴星的运动速率减小 | D. | 两星的运动周期保持不变 |
 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,则下列说法正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,则下列说法正确的是( )| A. | 带负电粒子从x1运动到x2电场力做负功 | |
| B. | x1、x2处电势小于零 | |
| C. | x1处的场强大于x2处的场强大小 | |
| D. | x1处的电势比x2处的电势低 |
| A. | 核电站发电 | B. | 氢弹爆炸 | C. | 石油的形成 | D. | 利用太阳能发电 |
 如图所示,一光滑的半径为R的半圆形轨道固定在水平面上,一个质量为m的小球以某一速度从半圆形轨道最低点A处冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,求(重力加速度为g )
如图所示,一光滑的半径为R的半圆形轨道固定在水平面上,一个质量为m的小球以某一速度从半圆形轨道最低点A处冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,求(重力加速度为g ) 如图所示,AB是竖直平面内的光滑四分之一圆弧轨道,O点是圆心,OA水平,B点是圆轨道的最低点,半径为R=0.2m.质量为M=1kg的物体乙静止在水平地面上,上表面水平,且上表面正好与圆弧轨道的B点相切,质量为m=0.5kg的物体甲(可视为质点)从A点由静止释放,已知甲与乙的动摩擦因数为μ1=0.5,乙与地面的动摩擦因数为μ2=0.1,重力加速度大小取10m/s2.
如图所示,AB是竖直平面内的光滑四分之一圆弧轨道,O点是圆心,OA水平,B点是圆轨道的最低点,半径为R=0.2m.质量为M=1kg的物体乙静止在水平地面上,上表面水平,且上表面正好与圆弧轨道的B点相切,质量为m=0.5kg的物体甲(可视为质点)从A点由静止释放,已知甲与乙的动摩擦因数为μ1=0.5,乙与地面的动摩擦因数为μ2=0.1,重力加速度大小取10m/s2.