题目内容
14．
如图所示为皮带传动装置，皮带轮的圆心分别为O、O′，A、C为皮带轮边缘上的点，B为A、O连线上的中点，RC=$\frac{1}{2}$RA，当皮带轮匀速转动时，皮带与皮带轮之间不打滑，求A、B、C三点的角速度之比、加速度之比分别为（ ）| A． | 1：1：2和2：1：4 | B． | 2：2：3和2：1：2 | C． | 1：1：2和1：2：1 | D． | 2：2：3和1：2：1 |
分析 两轮子靠传送带传动，轮子边缘上的点具有相同的线速度，共轴转动的点，具有相同的角速度，结合公式v=ωr列式分析角速度之比，再根据a=ω2r分析加速度之比．
解答 解：共轴转动的点，A与B具有相同的角速度，故ωA=ωB
A与C具有相等的线速度，根据公式v=ωR，v一定时，ω与R成反比，故：$\frac{{ω}_{A}}{{ω}_{C}}=\frac{{R}_{C}}{{R}_{A}}=\frac{1}{2}$，
故：ωA：ωB：ωC=1：1：2，
根据a=ω2r可知，aA：aB：aC=2：1：4，故A正确．
故选：A
点评 本题关键抓住同缘传动边缘上的点线速度相等、同轴传动角速度相同以及线速度与角速度关系公式v=ωr列式求解．
练习册系列答案
相关题目
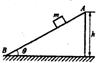如图所示，质量m=1kg的小滑块，由静止从倾角θ=37°的固定粗糙斜面顶端A滑至底端B，已知滑块与斜面间的动摩擦因数为μ=0.5，A点距离水平地面的高度为h=0.6m，（g=10m/s2），求：
如图，质量为m的小球b用长h的细绳悬挂于水平轨道BC的出口C处．质量也为m的小球a，从距BC高h的A处由静止释放，沿光滑轨道ABC滑下，在C处与b球正碰并与b粘在一起．已知BC轨道距地面的高度为0.5h．试问：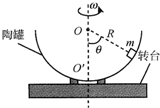
如图所示，半径为R的半球形容器，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过容器球心O的对称轴OO′重合，转台以一定的角速度ω匀速转动且相对容器壁静止，它和O点的连线与OO′之间的夹角θ为45°，重力加速度为g．
为了测量滑块与木板之间的动摩擦因数，采用如图所示装置：表面粗糙的木板固定在水平桌面上，左端装有定滑轮；木板上有一滑块，一端通过跨过定滑轮的细线与托盘连接，另一端与穿过打点计时器的纸带相连．实验中保持木板水平且细线平行于木板，在托盘中放入适量砝码后，滑块做匀加速直线运动，纸带上打出一系列的点．利用纸带测得滑块加速度为a，并已知重力加速度为g．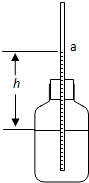
如图，在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管，瓶内有一定量的水和空气．由于内外压强差，细玻璃管内水面a将与瓶内水面有一定的高度差．已知地面附近高度每升高12m，大气压降低1mmHg；水银的密度为13.6×103kg/m3．