题目内容
13. 如图所示,一光滑的半径为R的半圆形轨道固定在水平面上,一个质量为m的小球以某一速度从半圆形轨道最低点A处冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,求(重力加速度为g )
如图所示,一光滑的半径为R的半圆形轨道固定在水平面上,一个质量为m的小球以某一速度从半圆形轨道最低点A处冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,求(重力加速度为g )(1)小球将要从轨道口飞出时的速度?
(2)小球落地点C距A处多远?
分析 (1)小球将要从轨道口飞出时,轨道的压力恰好为零,说明此时小球自身的重力大小恰好等于小球在此处需要的向心力,根据牛顿第二定律列式求解;
(2)从轨道口B处水平飞出后,小球做平抛运动,由平抛运动的规律可以求得C到A的距离.
解答 解:(1)小球将要从轨道口飞出时,轨道的压力恰好为零,说明此时小球自身的重力大小恰好等于小球在此处需要的向心力,有
$mg=m\frac{{v}^{2}}{R}$
因此小球在该位时刻的速度大小为$v=\sqrt{gR}$
(2)小球从轨道口飞出后将做平抛运动,H=2R=$\frac{1}{2}$gt2
而x=vt
解得:x=2R
答:(1)小球将要从轨道口飞出时的速度为$\sqrt{gR}$;
(2)小球落地点C距A处的距离为2R.
点评 本题是牛顿第二定律、平抛运动规律的综合运用问题,关键理清小球的运动情况,然后分阶段列式求解,难度适中.

练习册系列答案
相关题目
3. 质量相等的A、B两物体放在水平面上,分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的v-t图象如图所示.则下列说法正确的是( )
质量相等的A、B两物体放在水平面上,分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的v-t图象如图所示.则下列说法正确的是( )
 质量相等的A、B两物体放在水平面上,分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的v-t图象如图所示.则下列说法正确的是( )
质量相等的A、B两物体放在水平面上,分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的v-t图象如图所示.则下列说法正确的是( )| A. | A、B与水平面间的动摩擦因数之比为1:2 | |
| B. | F1、F2大小之比为1:2 | |
| C. | A、B两物体沿地面运动的位移之比为2:1 | |
| D. | 两物体A、B与地面摩擦产生的热量之比为1:2 |
1.当两个分子间的距离为r0时,正好处于平衡状态,下列关于分子间作用力与分子间距离的关系的说法正确的是( )
| A. | 当分子间的距离r<r0时,它们之间只有斥力作用 | |
| B. | 当分子间的距离r=r0时,分子处于平衡状态,分子不受力 | |
| C. | 当分子间的距离从0.5r0增大到10r0的过程中,分子间的引力和斥力都在减小,且斥力比引力减小得快 | |
| D. | 当分子间的距离从0.5r0增大到10r0的过程中,分子间相互作用力的合力在逐渐减小 |
8. 如图所示为用绞车拖物块的示意图.拴接物块的细线被缠绕在轮轴上,轮轴逆时针转动从而拖动物块.已知轮轴的半径R=1m,细线始终保持水平;被拖动物块质量m=10kg,与地面间的动摩擦因数μ=0.5;轮轴的角速度随时间变化的关系是ω=(4t)rad/s,g=10m/s2.以下判断正确的是( )
如图所示为用绞车拖物块的示意图.拴接物块的细线被缠绕在轮轴上,轮轴逆时针转动从而拖动物块.已知轮轴的半径R=1m,细线始终保持水平;被拖动物块质量m=10kg,与地面间的动摩擦因数μ=0.5;轮轴的角速度随时间变化的关系是ω=(4t)rad/s,g=10m/s2.以下判断正确的是( )
 如图所示为用绞车拖物块的示意图.拴接物块的细线被缠绕在轮轴上,轮轴逆时针转动从而拖动物块.已知轮轴的半径R=1m,细线始终保持水平;被拖动物块质量m=10kg,与地面间的动摩擦因数μ=0.5;轮轴的角速度随时间变化的关系是ω=(4t)rad/s,g=10m/s2.以下判断正确的是( )
如图所示为用绞车拖物块的示意图.拴接物块的细线被缠绕在轮轴上,轮轴逆时针转动从而拖动物块.已知轮轴的半径R=1m,细线始终保持水平;被拖动物块质量m=10kg,与地面间的动摩擦因数μ=0.5;轮轴的角速度随时间变化的关系是ω=(4t)rad/s,g=10m/s2.以下判断正确的是( )| A. | 物块做匀速运动 | |
| B. | 物块做匀加速直线运动,加速度大小是4m/s2 | |
| C. | 物块受到的摩擦力是50N | |
| D. | 绳对物块的拉力是90N |
18. 如图所示,光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角,与此同时对质点加上沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )
如图所示,光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角,与此同时对质点加上沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )
 如图所示,光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角,与此同时对质点加上沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )
如图所示,光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角,与此同时对质点加上沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )| A. | 因为有Fx,质点一定做曲线运动 | |
| B. | 如果Fy>Fx,质点向y轴一侧做曲线运动 | |
| C. | 如果Fy<Fxtan α,质点向x轴一侧做曲线运动 | |
| D. | Fy=Fx质点做直线运动 |
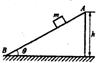 如图所示,质量m=1kg的小滑块,由静止从倾角θ=37°的固定粗糙斜面顶端A滑至底端B,已知滑块与斜面间的动摩擦因数为μ=0.5,A点距离水平地面的高度为h=0.6m,(g=10m/s2),求:
如图所示,质量m=1kg的小滑块,由静止从倾角θ=37°的固定粗糙斜面顶端A滑至底端B,已知滑块与斜面间的动摩擦因数为μ=0.5,A点距离水平地面的高度为h=0.6m,(g=10m/s2),求: 如图,质量为m的小球b用长h的细绳悬挂于水平轨道BC的出口C处.质量也为m的小球a,从距BC高h的A处由静止释放,沿光滑轨道ABC滑下,在C处与b球正碰并与b粘在一起.已知BC轨道距地面的高度为0.5h.试问:
如图,质量为m的小球b用长h的细绳悬挂于水平轨道BC的出口C处.质量也为m的小球a,从距BC高h的A处由静止释放,沿光滑轨道ABC滑下,在C处与b球正碰并与b粘在一起.已知BC轨道距地面的高度为0.5h.试问: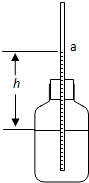 如图,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内水面有一定的高度差.已知地面附近高度每升高12m,大气压降低1mmHg;水银的密度为13.6×103kg/m3.
如图,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内水面有一定的高度差.已知地面附近高度每升高12m,大气压降低1mmHg;水银的密度为13.6×103kg/m3.