��Ŀ����
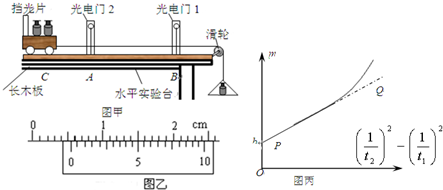
10��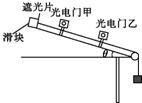 ��Ҫ����ͼ��ʾ��ʵ��װ��̽�������ܶ�������һ��Ǧȿɵ���б���ϰ�װ����������ţ����й�����ҹ̶���б���ϣ�����ż�λ�ÿ��ƶ��������쳤��ϸ��һ�˹̶��ڴ����ڹ�Ƭ������Ϊd���Ļ����ϣ���һ��ͨ���⻬������������������ϸ����б��ƽ�У�ͨ�����ֵ��ڣ�����������б���»�ʱ�������������ļ�ʱ��������ʾ�ڹ�Ƭ�����ʱ��t���Ӷ��ɲ������ͨ�������ʱ��˲ʱ�ٶ�v���ı����ż�λ�ã��ظ�ʵ�飬�Ƚ����������Ĺ�W��ϵͳ���ܵ�������Ek�Ĺ�ϵ�����ɴﵽʵ��Ŀ�ģ���Ҫʵ�鲽�����£�
��Ҫ����ͼ��ʾ��ʵ��װ��̽�������ܶ�������һ��Ǧȿɵ���б���ϰ�װ����������ţ����й�����ҹ̶���б���ϣ�����ż�λ�ÿ��ƶ��������쳤��ϸ��һ�˹̶��ڴ����ڹ�Ƭ������Ϊd���Ļ����ϣ���һ��ͨ���⻬������������������ϸ����б��ƽ�У�ͨ�����ֵ��ڣ�����������б���»�ʱ�������������ļ�ʱ��������ʾ�ڹ�Ƭ�����ʱ��t���Ӷ��ɲ������ͨ�������ʱ��˲ʱ�ٶ�v���ı����ż�λ�ã��ظ�ʵ�飬�Ƚ����������Ĺ�W��ϵͳ���ܵ�������Ek�Ĺ�ϵ�����ɴﵽʵ��Ŀ�ģ���Ҫʵ�鲽�����£���1������б�����Ǧȣ�����ƽ�⻬���Ħ�������������ڹ�Ƭ�Ļ�������б���ϣ����ƻ��飬ʹ֮�˶�������ͨ���ڹ�Ƭ����������ŵ�ʱ���Ƿ�����жϻ����Ƿ������������˶���
��2������Ƶķ�����װ��ʵ�����ģ��������Զ�����ż��϶��ɾ�ֹ�ͷţ�����ͨ������żס���ʱ���ڹ�Ƭ�����ʱ��ֱ�t1��t2����ͨ���ס����������ʱ��˲ʱ�ٶȷֱ�Ϊ$\frac{d}{{t}_{1}^{\;}}$��$\frac{d}{{t}_{2}^{\;}}$��
��3������ƽ������飨���ڹ�Ƭ��������M�����������m�����׳߲��������ż�ľ���x���Ƚ�mgx��$\frac{1}{2}��M+m����\frac{d}{{t}_{2}^{\;}}��_{\;}^{2}-\frac{1}{2}��M+m����\frac{d}{{t}_{1}^{\;}}��_{\;}^{2}$�Ĵ�С������������ķ�Χ�ڣ���������ȣ��ɵó����������������Ĺ��������嶯�ܵı仯����
���� ��1������$v=\frac{d}{t}$�����ڹ�Ƭ���һ������ɸ���ʱ��С���Ƿ�����ֱ���˶���
��2��Ӧ���ٶȹ�ʽ�������ͨ������ŵ�˲ʱ�ٶȣ�
��3��Ӧ�ö��ܶ������ʵ����Ҫ��֤�ı���ʽ��
��� �⣺��1�����������˶�ʱ���ڹ�Ƭ����������ŵ�ʱ����ȣ�
��2���ڹ�Ƭ����d��С������Ϊ��ƽ���ٶ��뻬��ͨ����λ��ʱ��˲ʱ�ٶ���ȣ��ʻ���ͨ���ס����������ʱ��˲ʱ�ٶȷֱ�Ϊ�ͣ�
${v}_{��}^{\;}=\frac{d}{{t}_{1}^{\;}}$��${v}_{��}^{\;}=\frac{d}{{t}_{2}^{\;}}$
��3���Ƚ���������mgx��ϵͳ���ܵ�����$\frac{1}{2}$��M+m��$[��\frac{d}{{t}_{2}^{\;}}��_{\;}^{2}-��\frac{d}{{t}_{1}^{\;}}��_{\;}^{2}]$�Ƿ���ȣ�����̽�������ܶ�������
�ʴ�Ϊ����1���ڹ�Ƭ����������ŵ�ʱ���Ƿ���ȡ�
��2��$\frac{d}{{t}_{1}^{\;}}$ $\frac{d}{{t}_{2}^{\;}}$
��3��mgx�� $\frac{1}{2}$��M+m��$[��\frac{d}{{t}_{2}^{\;}}��_{\;}^{2}-��\frac{d}{{t}_{1}^{\;}}��_{\;}^{2}]$
���� ���⿼���ˡ�̽�������������ٶȱ仯�Ĺ�ϵ������ȷ�˸�ʵ���ʵ��ԭ���Լ�ʵ��Ŀ�ģ������˽��������ĺ��壬�Լ���ν������ݴ�����

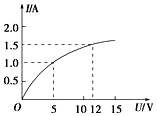
| A�� | ��5V��ѹʱ������ĵ�����0.2�� | |
| B�� | ��12V��ѹʱ������ĵ�����8�� | |
| C�� | ��ͼ��֪�����ŵ�ѹ��������ĵ��費�ϼ�С | |
| D�� | ��Ԫ��Ϊ������Ԫ��������ŷķ���ɲ����� |
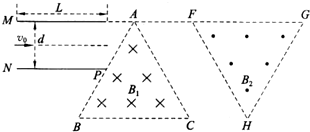
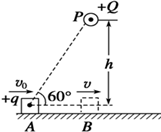 ��ͼ��ʾ�����㹻���Ĺ⻬��Եˮƽֱ�߹���Ϸ���P�㣬�̶�һ�����Ϊ+Q�ĵ��ɣ�һ����Ϊm���������Ϊ+q����飨����Ϊ�ʵ�ļ����ɣ����ӹ���ϵ�A���Գ��ٶ�v0�ع�������˶������˶���P�����·�B��ʱ�ٶ�Ϊv����֪���ɲ����ĵ糡��A��ĵ���Ϊ�գ�ȡ����Զ������Ϊ�㣩��P������������ֱ����Ϊh��P��A������ˮƽ����ļн�Ϊ60�㣬kΪ���糣��������˵����ȷ���ǣ�������
��ͼ��ʾ�����㹻���Ĺ⻬��Եˮƽֱ�߹���Ϸ���P�㣬�̶�һ�����Ϊ+Q�ĵ��ɣ�һ����Ϊm���������Ϊ+q����飨����Ϊ�ʵ�ļ����ɣ����ӹ���ϵ�A���Գ��ٶ�v0�ع�������˶������˶���P�����·�B��ʱ�ٶ�Ϊv����֪���ɲ����ĵ糡��A��ĵ���Ϊ�գ�ȡ����Զ������Ϊ�㣩��P������������ֱ����Ϊh��P��A������ˮƽ����ļн�Ϊ60�㣬kΪ���糣��������˵����ȷ���ǣ�������| A�� | �����A��ĵ�����EPA=Q�� | |
| B�� | �����A��ʱ�ܵ������֧������СΪmg+$\frac{3\sqrt{3}kqQ}{8{h}^{2}}$ | |
| C�� | ����+Q�����ĵ糡��B��ĵ糡ǿ�ȴ�СEB=K$\frac{q}{{h}^{2}}$ | |
| D�� | ����+Q�����ĵ糡��B��ĵ��Ʀ�B=$\frac{m}{2q}$��v02-v2��+�� |
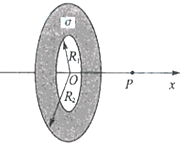 ͼʾΪһ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ���������жϣ�E�ĺ�������ʽӦΪ��������
ͼʾΪһ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ���������жϣ�E�ĺ�������ʽӦΪ��������| A�� | E=2��k�ң�$\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$��x | B�� | E=2��k�ң�$\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x | ||
| C�� | E=2��k�ң�$\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x | D�� | E=2��k�ң�$\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x |

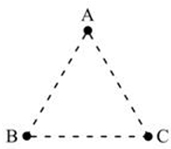 ��ͼ��ʾ������ǿ�糡����һ���ȱ�������ABC���ҵ糡��ƽ���ڸ�������ƽ�森��֪��A=2V����B=8V����C=4V������ͼ��������ͼ�л�����C��ĵ������A��ĵ糡�ߣ�
��ͼ��ʾ������ǿ�糡����һ���ȱ�������ABC���ҵ糡��ƽ���ڸ�������ƽ�森��֪��A=2V����B=8V����C=4V������ͼ��������ͼ�л�����C��ĵ������A��ĵ糡�ߣ�