题目内容
5. 如图所示,质量是M=4kg的木板静止在光滑水平面上,木板长为L0=8m,一个质量为m=1kg的小滑块以初速度V0=10m/s从左端滑上木板,由于滑块与木板间摩擦作用,木板也开始向右滑动,滑块滑到木板右端时二者恰好相对静止,求:
如图所示,质量是M=4kg的木板静止在光滑水平面上,木板长为L0=8m,一个质量为m=1kg的小滑块以初速度V0=10m/s从左端滑上木板,由于滑块与木板间摩擦作用,木板也开始向右滑动,滑块滑到木板右端时二者恰好相对静止,求:①二者相对静止时共同速度为多少?
②滑块与木板间的动摩擦因数多大?
分析 ①小滑块相对木板静止时,滑块与木板具有相同速度,根据牛顿第二定律和运动学公式求出共同速度;
②根据①求解的加速度,结合牛顿第二定律求解滑块与木板间的动摩擦因数.
解答 解:①设共同速度为v,m的位移:x1=v0t-$\frac{1}{2}$a1t2
M的位移:x2=$\frac{1}{2}$a1t2
位移关系:x1-x2=L0
速度关系:v=v0-a1t=a2t
根据牛顿第二定律有:f=ma1=Ma2
联立解得:v=2m/s,a1=5m/s2,a2=$\frac{5}{4}$m/s2
②根据牛顿第二定律有:μmg=ma1
解得:μ=0.5
答:①二者相对静止时共同速度为2m/s;
②滑块与木板间的动摩擦因数为0.5.
点评 本题主要考查了牛顿第二定律的应用,需要注意加速度是联系受力情况与运动情况的纽带.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
15.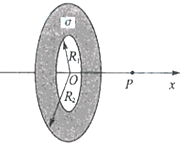 图示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.根据你的判断,E的合理表达式应为( )
图示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.根据你的判断,E的合理表达式应为( )
 图示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.根据你的判断,E的合理表达式应为( )
图示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.根据你的判断,E的合理表达式应为( )| A. | E=2πkσ($\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$)x | B. | E=2πkσ($\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$-$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x | ||
| C. | E=2πkσ($\frac{{R}_{1}}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x | D. | E=2πkσ($\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x |
10. 两个电荷量分别为+q和-q的带电粒子分别以速度Va和Vb射入匀强磁场,两粒子的入射方向与竖直磁场边界的夹角分别为30°和60°,磁场宽度为d,两粒子同时由A点出发,同时到达与A等高的B点,如图所示,则( )
两个电荷量分别为+q和-q的带电粒子分别以速度Va和Vb射入匀强磁场,两粒子的入射方向与竖直磁场边界的夹角分别为30°和60°,磁场宽度为d,两粒子同时由A点出发,同时到达与A等高的B点,如图所示,则( )
 两个电荷量分别为+q和-q的带电粒子分别以速度Va和Vb射入匀强磁场,两粒子的入射方向与竖直磁场边界的夹角分别为30°和60°,磁场宽度为d,两粒子同时由A点出发,同时到达与A等高的B点,如图所示,则( )
两个电荷量分别为+q和-q的带电粒子分别以速度Va和Vb射入匀强磁场,两粒子的入射方向与竖直磁场边界的夹角分别为30°和60°,磁场宽度为d,两粒子同时由A点出发,同时到达与A等高的B点,如图所示,则( )| A. | a粒子带正电,b粒子带负电 | B. | 两粒子的轨道半径之比Ra:Rb=1:$\sqrt{3}$ | ||
| C. | 两粒子的质量之比ma:mb=1:2 | D. | 两粒子的速度之比Va:Vb=2:$\sqrt{3}$ |
17.下列关于时间和时刻的两种说法意义相同的是( )
| A. | 第2 s末和第3 s初 | B. | 前3 s内和第3 s内 | ||
| C. | 第3 s末和第2 s初 | D. | 第1 s内和第1 s末 |
15.一质点沿某一直线做匀变速直线运动,先后通过a、b两点,该质点通过ab全程的平均速度大小为v1,其中间时刻的瞬时速度大小为v2,中点位置的瞬时速度大小为v3.关于这三个速度的大小,下列说法正确的是( )
| A. | 若质点做匀加速直线运动,则v1=v2<v3 | |
| B. | 若质点做匀加速直线运动,则v1<v2<v3 | |
| C. | 若质点做匀减速直线运动,则v1=v2<v3 | |
| D. | 若质点做匀减速直线运动,则v1=v2>v3 |
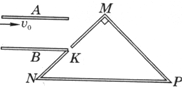 如图所示,水平放置的平行金属板A和B的间距为d,极板长为2d;金属板右侧有三块挡板MN,NP,PM围成一个等腰直角三角形区域,顶角∠NMP=90°,MN挡板上的中点处有一个小孔K恰好位于B板右端,已知水平挡板NP的长度为$\overline{NP}$=2$\sqrt{2}$a.由质量为m、带电量为+q的同种粒子组成的粒子束,以速度v0从金属板A、B左端沿板A射人,不计粒子所受的重力,若在A、B板间加一恒定电压,使粒子穿过金属板后恰好打到小孔K.求:
如图所示,水平放置的平行金属板A和B的间距为d,极板长为2d;金属板右侧有三块挡板MN,NP,PM围成一个等腰直角三角形区域,顶角∠NMP=90°,MN挡板上的中点处有一个小孔K恰好位于B板右端,已知水平挡板NP的长度为$\overline{NP}$=2$\sqrt{2}$a.由质量为m、带电量为+q的同种粒子组成的粒子束,以速度v0从金属板A、B左端沿板A射人,不计粒子所受的重力,若在A、B板间加一恒定电压,使粒子穿过金属板后恰好打到小孔K.求: 某学习小组欲验证动能定理,他们在实验室找到了打点计时器、学生电源、导线、细线、复写纸、纸带、长木板、滑块、沙及沙桶,组装了一套如图所示的实验验证装置.
某学习小组欲验证动能定理,他们在实验室找到了打点计时器、学生电源、导线、细线、复写纸、纸带、长木板、滑块、沙及沙桶,组装了一套如图所示的实验验证装置.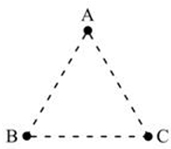 如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形平面.已知φA=2V,φB=8V,φC=4V.用作图法,请在图中画出过C点的等势面和过A点的电场线.
如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形平面.已知φA=2V,φB=8V,φC=4V.用作图法,请在图中画出过C点的等势面和过A点的电场线. 如图所示,一轻杆AB把一重力为G的光滑球夹在墙的中间,杆与墙的夹角θ=300,杆的B端用绞链固定在墙上,杆的A端用绳子水平拉住,D点为球与杆的接触点,D为杆AB的中点,求墙对杆B端的作用力.
如图所示,一轻杆AB把一重力为G的光滑球夹在墙的中间,杆与墙的夹角θ=300,杆的B端用绞链固定在墙上,杆的A端用绳子水平拉住,D点为球与杆的接触点,D为杆AB的中点,求墙对杆B端的作用力.