题目内容
2. 如图所示,在固定斜面上有两个完全相同的小球a和b,两球从顶端滑到底端,a球由静止开始下滑,b球以水平速度v0紧贴斜面抛出,则下列说法中正确的是( )
如图所示,在固定斜面上有两个完全相同的小球a和b,两球从顶端滑到底端,a球由静止开始下滑,b球以水平速度v0紧贴斜面抛出,则下列说法中正确的是( )| A. | 若斜面光滑,a、b两球滑到底端所用的时间ta=tb | |
| B. | 若斜面光滑,a、b两球滑到底端时重力的功率相同 | |
| C. | 若斜面粗糙,a、b两球滑到底端所用的时间ta>tb | |
| D. | 若斜面粗糙,a、b两球滑到底端所用的时间ta<tb |
分析 将b球的运动分解为沿斜面向下的运动和水平方向的运动,根据运动的独立性判断运动时间,沿斜面方向的速度;求得重力的功率;
解答 解:A、若斜面光滑,将b球的运动分解为沿斜面向下的运动和水平方向的运动,沿斜面方向两球的运动情况相同,故同时到达底端,故A正确
B、若斜面光滑,将b球的运动分解为沿斜面向下的运动和水平方向的运动,沿斜面方向两球的运动情况相同,故到达斜面底端的沿斜面的速度相同,重力的功率,P=mgv相同,故B正确;
C、若斜面粗糙,a球的加速度沿斜面向下为gsinθ-μmgcosθ,将b球的运动分解为沿斜面向下的运动和水平方向的运动,b球沿斜面向下的加速度为gsinθ-μmgcosθsinα,(α为b球运动方向与水平方向的夹角)故b球的加速度大,由h=$\frac{1}{2}a{t}^{2}$得滑到底端所用的时间ta>tb,故C正确、D错误.
故选:ABC
点评 本题考查机械能守恒定律以及运动的合成和分解规律的应用,要注意明确34两物体的运动可视为类平抛运动,根据运动的合成和分解规律求解

练习册系列答案
相关题目
13.科学家设想在太空设立太阳能卫星电站,卫星电站的最佳位置是在赤道上空1100km的圆轨道上,那么此卫星电站比近地表面附近圆轨道上的卫星( )
| A. | 线速度大 | B. | 角速度大 | C. | 周期大 | D. | 向心加速度大 |
17.银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,且S1的质量大于S2,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.关于这对双星的运动说法正确的是( )
| A. | S1的运动周期大于S2 | B. | S1的向心力大于S2 | ||
| C. | S1的速度小于S2 | D. | S1的加速度小于S2 |
7.如图甲所示,是由两块粗糙程度不同的木板A、B平滑连接在一起,其中A板倾角可调.现让一滑块从高h处由静止滑下,在水平板上滑行x后停止运动.改变h大小但保持距离d不变的情况下描绘出的x-h图象如图乙所示.则滑块与木板A、B间的动摩擦因数分别为( )


| A. | $\frac{a}{d}$,$\frac{a}{b}$ | B. | $\frac{a}{b}$,$\frac{a}{d}$ | C. | $\frac{d}{a}$,$\frac{b}{a}$ | D. | $\frac{b}{a}$,$\frac{d}{a}$ |
14.美国航空航天局2009年6月发射了“月球勘测轨道器”(LRO),LRO每天在离月球表面50km的高度穿越月球两极上空10次.若以T表示LRO在离月球表面高度h处的轨道上做匀速圆周运动的周期,以R表示月球的半径,则( )
| A. | 月球表面的重力加速度为$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}{R}^{2}}$ | |
| B. | 月球表面的重力加速度为$\frac{4{π}^{2}(R+h)}{{T}^{2}}$ | |
| C. | LRO运行时的向心加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| D. | LRO运行时的向心加速度为$\frac{4{π}^{2}(R+h)^{2}}{{T}^{2}}$ |
11.如图所示,虚线框内为漏电保护开关的原理示意图,变压器A处用火线和零线平行绕制成线圈,然后接到用电器,B处有一个输电线圈,一旦线圈B中有电流,经过放大后便能推动继电器切断电源,如果甲、乙、丙、丁四人分别以图示方式接触电线(裸露部分),甲、乙、丙站在木凳上,则下列说法正确的是( )


| A. | 甲不会发生触电事故,继电器不会切断电源 | |
| B. | 乙会发生触电事故,继电器不会切断电源 | |
| C. | 丙会发生触电事故,继电器会切断电源 | |
| D. | 丁会发生触电事故,继电器会切断电源 |
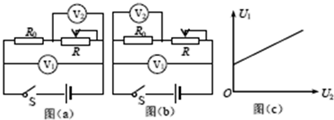
 某研究性学习小组探究小灯泡灯丝电阻与温度的关系,主要仪器有:
某研究性学习小组探究小灯泡灯丝电阻与温度的关系,主要仪器有: