题目内容
3.某实验小组用图甲所示装置来研究匀变速直线运动规律.图乙是在长木板水平放置时得到的一根打点清晰的纸带,每隔4个打下的点选取一个计数点,测出相邻计数点间的距离并标注在纸带上.已知打点计时器使用交变电源的频率为50Hz.不计滑轮与轮轴间的摩擦,重力加速度取g=10m/s2,则:(1)打计数点3时,小车的速度为v3=0.6m/s,小车加速过程中的加速度a1=2m/s2.
(2)由数据分析可知,小车在一段时间内作减速运动,造成这种现象的原因是钩码在到达滑轮前已经落地.
(3)请根据测得的数据,求出此次试验中小车质量M与钩码质量m的比值$\frac{M}{m}$=$\frac{8}{3}$.

(4)该小组还利用图甲所示装置探究加速度与力的关系:平衡摩擦力后,保持小车质量不变,分别挂不同数目的钩码以改变拉力,测出小车对应的加速度,并作出小车的加速度a与对应所挂钩码个数n的图象如图丙,根据图象中AB段为直线可得出的结论是小车的加速度与所受的合力成正比.造成图象中BC段弯曲的原因是钩码的质量不满足远小于小车的质量.
分析 根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上3点时小车的瞬时速度大小.根据牛顿第二定律分析m和M进行求解.
解答 解:(1)每隔4个打下的点选取一个计数点,所以相邻的计数点间的时间间隔T=0.1s,
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上3点时小车的瞬时速度大小.
v3=$\frac{5.00+7.00}{2×0.1}$=0.6m/s
根据纸带可以得到加速过程相邻计数点间的位移之差相等,即△x=2cm,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:a=$\frac{2×1{0}^{-2}}{0.{1}^{2}}$=2m/s2.
(2)由数据分析可知,小车在一段时间内作减速运动,造成这种现象的原因是钩码在小车到达滑轮前已落地.
(3)根据减速运动得纸带数据得出做减速运动的加速度大小a′=$\frac{1×1{0}^{-2}}{0.{1}^{2}}$=1m/s2.
根据牛顿第二定律分析m和M得:
m:mg-F=ma
M:F-f=Ma,f=Ma′
解得:小车质量M与钩码质量m的比值$\frac{M}{m}$=$\frac{8}{3}$.
(4)根据图象中AB段为直线可得出的结论是小车的加速度与所受的合力成正比.
随着外力F的增大,钩码的质量越来越大,最后出现了不满足远小于小车质量的情况,因此图线出现了偏折现象,
所以造成图象中BC段弯曲的原因是钩码的质量不满足远小于小车的质量.
故答案为:(1)0.6,2;(2)钩码在到达滑轮前已经落地;
(3)$\frac{8}{3}$;
(4)小车的加速度与所受的合力成正比,钩码的质量不满足远小于小车的质量.
点评 要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.了解实验的操作步骤和数据处理以及注意事项,尤其是理解平衡摩擦力和M>>m的操作和要求的含义.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案| A. | 物体的运动状态发生变化,物体的受力情况一定变化 | |
| B. | 物体的运动状态保持不变,说明物体所受的合外力为零 | |
| C. | 物体在恒力作用下,一定做匀变速直线运动 | |
| D. | 物体做曲线运动时,受到的合外力可以是恒力 |
 如图所示,质量M=4kg长为L=10m的木板停放在光滑水平面上,另一不计长度、质量m=1kg的木块以某一速度从右端滑上木板,木板与木块间的动摩擦因数μ=0.8.若要使木板获得的速度不大于2m/s,木块的初速度v0应满足的条件为(g取10/s2)( )
如图所示,质量M=4kg长为L=10m的木板停放在光滑水平面上,另一不计长度、质量m=1kg的木块以某一速度从右端滑上木板,木板与木块间的动摩擦因数μ=0.8.若要使木板获得的速度不大于2m/s,木块的初速度v0应满足的条件为(g取10/s2)( )| A. | v0≥10 m/s | B. | v0≤10 m/s | C. | v0≥15 m/s | D. | v0≤15 m/s |
| A. | 物体在计时开始时刻的速度为零 | B. | 物体在2s末的速度为2.5m/s | ||
| C. | 物体的加速度大小为2m/s2 | D. | 物体在前4s内的平均速度为2m/s |
| A. | 当沿运动方向油滴始终均匀分布时,车一定做匀速直线运动 | |
| B. | 当沿运动方向油滴间距逐渐增大时,车一定在做匀加速直线运动 | |
| C. | 当沿运动方向油滴间距逐渐增大时,车的加速度可能在减小 | |
| D. | 当沿运动方向油滴间距逐渐增大时,车的加速度一定在增大 |
 2016年9月15日22时04分,我国在酒泉卫星发射中心用长征二号FT2运载火箭将天宫二号空间实验室发射升空.已知天宫二号在驶向既定轨道Ⅰ过程中,在A点从椭圆形轨道Ⅱ进入圆形轨道Ⅰ,B为轨道Ⅱ上的一点,且离地球表面距离相对很小,如图所示,关于天宫二号的运动,下列说法中正确的是( )
2016年9月15日22时04分,我国在酒泉卫星发射中心用长征二号FT2运载火箭将天宫二号空间实验室发射升空.已知天宫二号在驶向既定轨道Ⅰ过程中,在A点从椭圆形轨道Ⅱ进入圆形轨道Ⅰ,B为轨道Ⅱ上的一点,且离地球表面距离相对很小,如图所示,关于天宫二号的运动,下列说法中正确的是( )| A. | 在轨道Ⅱ上经过A时,天宫二号需要减速才可进入轨道Ⅰ | |
| B. | 在轨道Ⅱ上运行周期小于轨道Ⅰ上运行周期 | |
| C. | 在轨道Ⅱ上,经过A的加速度小于经过B的加速度 | |
| D. | 在B点时,航天飞机的速度大于7.9km/s |
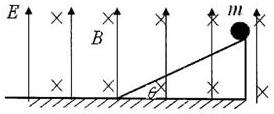 如图所示,空间内存在垂直纸面向里的匀强磁场和竖直向上的匀强电场,一带电小球(可视为质点)质量m=0.4kg,电荷量q=-0.8C,从倾角θ=37°的光滑斜面最高点由静止开始下滑,当沿斜面下滑距离s=$\frac{8}{3}$m时与斜面脱离.此时立即将电场反向,小球做匀速圆周运动,最终恰好不与地面发生碰撞,重力加速度g=10m/s2.求:
如图所示,空间内存在垂直纸面向里的匀强磁场和竖直向上的匀强电场,一带电小球(可视为质点)质量m=0.4kg,电荷量q=-0.8C,从倾角θ=37°的光滑斜面最高点由静止开始下滑,当沿斜面下滑距离s=$\frac{8}{3}$m时与斜面脱离.此时立即将电场反向,小球做匀速圆周运动,最终恰好不与地面发生碰撞,重力加速度g=10m/s2.求: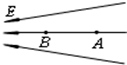 如图是电场中某区域的电场线分布图,A,B是电场中的两点,可以判断该电场的方向是向左(选填“向左”或“向右”),可以判断A点场强较小(选填“A”或“B”);一正点电荷在B点受到电场力的方向是向左(选填“向 左”或“向右”).
如图是电场中某区域的电场线分布图,A,B是电场中的两点,可以判断该电场的方向是向左(选填“向左”或“向右”),可以判断A点场强较小(选填“A”或“B”);一正点电荷在B点受到电场力的方向是向左(选填“向 左”或“向右”).