题目内容
14. 所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA 偏离竖直方向37°角,PB在水平方向,且连在所受重力G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,已知sin 37°=0.6,cos 37°=0.8,重力加速度g取10m/s2.求木块受到斜面对它的摩擦力Ff和支持力FN各为多大?
所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA 偏离竖直方向37°角,PB在水平方向,且连在所受重力G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,已知sin 37°=0.6,cos 37°=0.8,重力加速度g取10m/s2.求木块受到斜面对它的摩擦力Ff和支持力FN各为多大?
分析 先以结点P为研究对象,分析受力情况,由平衡条件求出BP绳的拉力大小,再以G2为研究对象,分析受力,作出力图,根据平衡条件求解斜面对木块的摩擦力和弹力.
解答  解:分析P点受力情况如图乙所示,由平衡条件可得:
解:分析P点受力情况如图乙所示,由平衡条件可得:
FAcos 37°=G1
FAsin 37°=FB
可解得:FB=6N
对木块进行受力分析如图丙所示.
由物体的平衡条件可得:
Ff=G2sin 37°+FB'cos 37°
FN+FB'sin 37°=G2cos 37°
FB'=FB
可求得:Ff=64.8N
FN=76.4N.
答:木块受到斜面对它的摩擦力Ff为64.8N,支持力FN为76.4N.
点评 本题是通过绳子连接的物体平衡问题,采用隔离法研究是基本方法.要作好力图,这是解题的基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.预计在2020年前后,中国将在轨组装载人空间站.已知空间站绕月球做匀速圆周运动的轨道半径为r,月球的半径为R,月球表面的重力加速度为g,下列说法正确的是( )
| A. | 空间站的线速度v=$\sqrt{\frac{g{r}^{2}}{R}}$ | B. | 空间站的角速度ω=$\sqrt{\frac{g{R}^{3}}{{r}^{2}}}$ | ||
| C. | 空间站的加速度a=$\sqrt{\frac{g{R}^{2}}{{r}^{2}}}$ | D. | 空间站的周期T=2π$\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$ |
6. 某空间存在着如图所示的水平方向的匀强磁场,A、B两个物块叠放在一起,并置于粗糙的水平地面上.物块A带正电,物块B为不带电的绝缘物块.水平恒力F作用在物块B上,使A、B一起由静止开始向左运动,则此后的过程中( )
某空间存在着如图所示的水平方向的匀强磁场,A、B两个物块叠放在一起,并置于粗糙的水平地面上.物块A带正电,物块B为不带电的绝缘物块.水平恒力F作用在物块B上,使A、B一起由静止开始向左运动,则此后的过程中( )
 某空间存在着如图所示的水平方向的匀强磁场,A、B两个物块叠放在一起,并置于粗糙的水平地面上.物块A带正电,物块B为不带电的绝缘物块.水平恒力F作用在物块B上,使A、B一起由静止开始向左运动,则此后的过程中( )
某空间存在着如图所示的水平方向的匀强磁场,A、B两个物块叠放在一起,并置于粗糙的水平地面上.物块A带正电,物块B为不带电的绝缘物块.水平恒力F作用在物块B上,使A、B一起由静止开始向左运动,则此后的过程中( )| A. | A对B的压力变小 | B. | B对地面的压力先变大后不变 | ||
| C. | B对A的摩擦力不变 | D. | 最终A将落到B的后面 |
4.一辆汽车从静止开始沿直线匀加速开出,然后保持匀速运动,最后做匀减速运动直到停止,表给出了不同时刻汽车的速度,据此表可以判断( )
| 时刻(s) | 2.0 | 4.0 | 6.0 | 10.0 | 12.0 | 14.0 | 19.0 | 21.0 |
| 速度(m/s) | 3 | 6 | 9 | 12 | 12 | 12 | 9 | 3 |
| A. | 汽车做匀加速运动时的加速度大小为1.5 m/s2 | |
| B. | 汽车匀加速运动的时间为6 s | |
| C. | 汽车匀速运动的时间为4 s | |
| D. | 汽车总共通过的路程为192 m |
 在“验证机械能守恒定律”的实验中,质量m=1kg的重锤自由下落,在纸袋上打出一系列的点,如图所示,相邻计数点时间间隔为0.02s,打点计时器所用交流电源频率为50Hz,当地重力加速度的值为9.80m/s2.那么,从起点O到打下计数点B的过程中:重力势能减少量是△Ep=0.51J,物体动能的增加量△Ek=0.48J(均取两位有效数字)
在“验证机械能守恒定律”的实验中,质量m=1kg的重锤自由下落,在纸袋上打出一系列的点,如图所示,相邻计数点时间间隔为0.02s,打点计时器所用交流电源频率为50Hz,当地重力加速度的值为9.80m/s2.那么,从起点O到打下计数点B的过程中:重力势能减少量是△Ep=0.51J,物体动能的增加量△Ek=0.48J(均取两位有效数字) 一个电子以v0=4×107m/s的速度,方向与电场方向相同,射入电场强度E=2×105V/m的匀强电场中,如图所示,已知电子电量-e=-1.6×10-19C,电子质量m=9.1×10-31kg.试求:
一个电子以v0=4×107m/s的速度,方向与电场方向相同,射入电场强度E=2×105V/m的匀强电场中,如图所示,已知电子电量-e=-1.6×10-19C,电子质量m=9.1×10-31kg.试求:
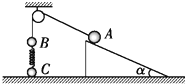 如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A小球放在固定的光滑斜面上,斜面的倾角为α,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C小球放在水平地面上.现用手控制A小球,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知B、C两小球的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计.
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A小球放在固定的光滑斜面上,斜面的倾角为α,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C小球放在水平地面上.现用手控制A小球,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知B、C两小球的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计. 如图所示,传送带与水平面的夹角θ=37°,并以4m/s的速度向上运行,在传送带的底端A处无初速度地放上一个质量为0.5kg的物体,它与传送带间动摩擦因数μ=0.8,物体从底端A到顶端B所用时间t=11.25s.若已知sin 37°=0.6,cos 37°=0.8,g=10m/s2,则AB间长度x为多少?
如图所示,传送带与水平面的夹角θ=37°,并以4m/s的速度向上运行,在传送带的底端A处无初速度地放上一个质量为0.5kg的物体,它与传送带间动摩擦因数μ=0.8,物体从底端A到顶端B所用时间t=11.25s.若已知sin 37°=0.6,cos 37°=0.8,g=10m/s2,则AB间长度x为多少?