题目内容
18. 如图所示,半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的质点自轨道端点P由静止开始滑下,自P滑到Q的过程中,克服摩擦力所做的功为$\frac{1}{2}$mgR,重力加速度大小为g,质点滑到最低点Q时对轨道的正压力为( )
如图所示,半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的质点自轨道端点P由静止开始滑下,自P滑到Q的过程中,克服摩擦力所做的功为$\frac{1}{2}$mgR,重力加速度大小为g,质点滑到最低点Q时对轨道的正压力为( )| A. | mg | B. | $\frac{mg}{4}$ | C. | $\frac{mg}{2}$ | D. | 2mg |
分析 对P滑到Q的过程运用动能定理,求出质点在最低点的速度.在最低点,根据牛顿第二定律求出轨道对质点的支持力,从而得到质点对轨道的压力.
解答 解:P到Q的过程,根据动能定理得
mgR-Wf=$\frac{1}{2}$mv2
据题 Wf=$\frac{1}{2}$mgR
在Q点,根据牛顿第二定律得,N-mg=m$\frac{{v}^{2}}{R}$
联立解得 N=2mg,由牛顿第三定律知,质点滑到最低点Q时对轨道的正压力为2mg.
故选:D
点评 本题考查了动能定理和牛顿第二定律的基本运用,通过牛顿第二定律求出最低点的速度是解决本题的关键.

练习册系列答案
相关题目
18.质量不同而具有相同初动能的两个物体,从地球表面竖直向上抛出.上升过程中,当上升到同一高度时(不计空气阻力),它们( )
| A. | 具有的重力势能相等 | B. | 所具有的机械能相等 | ||
| C. | 重力做的功不相等 | D. | 所具有的动能相等 |
3.质量为m的物体,由静止开始下落,由于阻力作用,下落的加速度为$\frac{4}{5}$g,在物体下落h的过程中,下列说法正确的是( )
| A. | 物体的重力势能减少了$\frac{4}{5}$mgh | B. | 物体的机械能减少了$\frac{4}{5}$mgh | ||
| C. | 物体的动能增加了$\frac{4}{5}$mgh | D. | 物体克服阻力所做的功为$\frac{4}{5}$mgh |
10.下列关于质点的认识,正确的是( )
| A. | 质量小的物体一定能视为质点 | |
| B. | 体积小的物体一定能视为质点 | |
| C. | 研究地球自转时能把地球视为质点 | |
| D. | 研究地球绕太阳公转时能把地球视为质点 |
7. 王老师讲了一个龟兔沿直线赛跑的新编故事.按照王老师讲的故事情节.李明同学正确地画出了兔子的位移--时间图象如图所示,关于兔子的运动情况,下列说法正确的是( )
王老师讲了一个龟兔沿直线赛跑的新编故事.按照王老师讲的故事情节.李明同学正确地画出了兔子的位移--时间图象如图所示,关于兔子的运动情况,下列说法正确的是( )
 王老师讲了一个龟兔沿直线赛跑的新编故事.按照王老师讲的故事情节.李明同学正确地画出了兔子的位移--时间图象如图所示,关于兔子的运动情况,下列说法正确的是( )
王老师讲了一个龟兔沿直线赛跑的新编故事.按照王老师讲的故事情节.李明同学正确地画出了兔子的位移--时间图象如图所示,关于兔子的运动情况,下列说法正确的是( )| A. | 从0到t1时刻,作匀速直线运动 | B. | 从t1到t2时刻,作匀速直线运动 | ||
| C. | 从t2到t3时刻,作匀速直线运动 | D. | 从t3到t4时刻,作匀加速直线运动 |
8.运动员将网球水平击出,球未触网落到对方场地,已知击球点离地面的高度为1.8m,重力加速度取10m/s2,则球在空中的飞行时间大约是( )
| A. | 0.6s | B. | 0.36s | C. | 5s | D. | 0.18s |
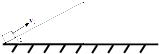 如图所示,斜劈固定放置在水平地面上,它的斜面长度L=3.4m,倾角为α=30°.从某时刻起,一木块(可视为质点)以v0=10m/s的初速度从斜面底端沿平行斜面方向冲上斜面,木块与斜面间的动摩擦因数$μ=\frac{{\sqrt{3}}}{2}$,空气阻力不计,重力加速度g取10m/s2.求木块冲出斜面后刚接触地面时的速率v.
如图所示,斜劈固定放置在水平地面上,它的斜面长度L=3.4m,倾角为α=30°.从某时刻起,一木块(可视为质点)以v0=10m/s的初速度从斜面底端沿平行斜面方向冲上斜面,木块与斜面间的动摩擦因数$μ=\frac{{\sqrt{3}}}{2}$,空气阻力不计,重力加速度g取10m/s2.求木块冲出斜面后刚接触地面时的速率v.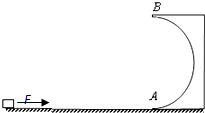 半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为u=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问:
半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为u=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问: