题目内容
13.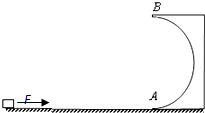 半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为u=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问:
半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为u=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问:(1)滑块到达B点时速度大小;
(2)滑块在B处对轨道的压力;
(3)滑块通过B点后的落地点到B点的水平距离.
分析 (1)滑块从A到B,F做功为Fx,滑动摩擦力为-μmgx,重力做功为-2mgR,根据动能定理求解小物块到达B点时速度的大小;
(2)在B处,由合力提供向心力,由牛顿第二定律求解轨道对滑块作用力的大小,再由牛顿第三定律得到滑块对轨道的压力大小;
(3)滑块离开B点后做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由运动学公式求解落到水平地面上的点与B点之间的水平距离.
解答 解:(1)从A到B,根据动能定理有:
(F-μmg)x-2mgR=$\frac{1}{2}m{v}_{B}^{2}$
得:vB=$\sqrt{\frac{2(F-μmg)x}{m}-4gR}$=$\sqrt{\frac{2×(11-0.2×0.5×10)×1.3}{0.5}-4×10×0.9}$=4m/s
(2)在B点,根据牛顿第二定律有:F+mg=m$\frac{{v}_{B}^{2}}{R}$
解得:F=m($\frac{{v}_{B}^{2}}{R}$-g)=0.5×($\frac{{4}^{2}}{0.9}$-10)=$\frac{35}{9}$N
由牛顿第三定律得,滑块在B处对轨道的压力为:F′=F=$\frac{35}{9}$N
(3)由B点到落点滑块做平抛运动,在竖直方向有:
2R=$\frac{1}{2}$gt2
得:t=2$\sqrt{\frac{R}{g}}$=2×$\sqrt{\frac{0.9}{10}}$=0.6s
水平面上落点与B点之间的水平距离为:x=vBt=4×0.6=2.4m
答:(1)滑块到达B点时速度大小是4m/s;
(2)滑块在B处对轨道的压力是$\frac{35}{9}$N;
(3)滑块通过B点后的落地点到B点的水平距离是2.4m.
点评 本题的关键要理清滑块的运动过程,把握每个过程的物理规律,运用动能定理、牛顿第二定律和平抛运动规律进行研究.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案 如图所示,重10N的滑块在倾角为30°的斜面上,从a点由静止下滑,到b点接触到一个轻弹簧,滑块压缩弹簧到c点开始弹回,返回b点离开弹簧,最后又回到a点,已知ab=0.8m,bc=0.4m,那么在整个过程中( )
如图所示,重10N的滑块在倾角为30°的斜面上,从a点由静止下滑,到b点接触到一个轻弹簧,滑块压缩弹簧到c点开始弹回,返回b点离开弹簧,最后又回到a点,已知ab=0.8m,bc=0.4m,那么在整个过程中( )| A. | 滑块滑到b点时动能最大 | |
| B. | 滑块动能的最大值是6J | |
| C. | 从c到b弹簧的弹力对滑块做的功是6J | |
| D. | 滑块和弹簧组成的系统在整个过程中机械能守恒 |

| A. | am=40m/s2 h=3.2m | B. | am=40m/s2 h=3.0m | ||
| C. | am=20m/s2 h=3.2m | D. | am=20m/s2 h=3.0m |
 刀、斧、凿等切削工具的刃部叫做劈,如图是用斧头劈木柴的示意图.劈的纵截面是一个等腰三角形,使用劈的时候,垂直劈背上加一力 F,这个力产生两个作用效果,使劈的两个侧面推压物体,把木柴劈开.设劈背的宽度为d,劈的斜面长为l,不计斧头的自身重力,则劈的侧面推压木柴的力约为( )
刀、斧、凿等切削工具的刃部叫做劈,如图是用斧头劈木柴的示意图.劈的纵截面是一个等腰三角形,使用劈的时候,垂直劈背上加一力 F,这个力产生两个作用效果,使劈的两个侧面推压物体,把木柴劈开.设劈背的宽度为d,劈的斜面长为l,不计斧头的自身重力,则劈的侧面推压木柴的力约为( )| A. | $\frac{d}{l}$F | B. | $\frac{l}{d}$F | C. | $\frac{l}{2d}$F | D. | $\frac{d}{2l}$F |
 如图所示,半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的质点自轨道端点P由静止开始滑下,自P滑到Q的过程中,克服摩擦力所做的功为$\frac{1}{2}$mgR,重力加速度大小为g,质点滑到最低点Q时对轨道的正压力为( )
如图所示,半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的质点自轨道端点P由静止开始滑下,自P滑到Q的过程中,克服摩擦力所做的功为$\frac{1}{2}$mgR,重力加速度大小为g,质点滑到最低点Q时对轨道的正压力为( )| A. | mg | B. | $\frac{mg}{4}$ | C. | $\frac{mg}{2}$ | D. | 2mg |
 如图(甲)所示,荡秋千是一种常见的娱乐休闲活动,小女孩荡秋千的运动过程可用图(乙)示意.忽略空气阻力和一切摩擦,小女孩从最高点A摆到最低点B的过程( )
如图(甲)所示,荡秋千是一种常见的娱乐休闲活动,小女孩荡秋千的运动过程可用图(乙)示意.忽略空气阻力和一切摩擦,小女孩从最高点A摆到最低点B的过程( )| A. | 重力势能增加 | B. | 动能增加 | C. | 机械能增加 | D. | 机械能减少 |
| A. | 法拉第和爱迪生 | B. | 麦克斯韦和赫兹 | C. | 奥斯特和贝尔 | D. | 法拉第和赫兹 |
 如图所示,轻弹簧的一端固定在地面上,另一端与木块B相连,木块A放在B上,两木块的质量均为m,在竖直向下的力F作用下,A、B均静止,然后将力F突然撤去,之后的运动过程中A、B始终不分离,重力加速度为g,问:
如图所示,轻弹簧的一端固定在地面上,另一端与木块B相连,木块A放在B上,两木块的质量均为m,在竖直向下的力F作用下,A、B均静止,然后将力F突然撤去,之后的运动过程中A、B始终不分离,重力加速度为g,问: