题目内容
18. 如图所示,正方形容器处在匀强磁场中,一束电子从a孔沿a→b方向垂直射入容器内的匀强磁场中,结果一部分电子从小孔c竖直射出,一部分电子从小孔d水平射出,则以下叙述正确的是( )
如图所示,正方形容器处在匀强磁场中,一束电子从a孔沿a→b方向垂直射入容器内的匀强磁场中,结果一部分电子从小孔c竖直射出,一部分电子从小孔d水平射出,则以下叙述正确的是( )| A. | 从c、d两孔射出的电子在容器中运动的时间之比tc:td=1:2 | |
| B. | 从c、d两孔射出的电子在容器中运动的时间之比tc:td=2:1 | |
| C. | 在容器中运动的加速度大小之比ac:ad=1:2 | |
| D. | 在容器中运动的加速度大小之比ac:ad=2:1 |
分析 带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,有Bqv=m$\frac{{v}^{2}}{r}$,得出半径公式r=$\frac{mv}{Bq}$,根据半径关系得出粒子的速度关系.再根据${a}_{n}=\frac{{v}^{2}}{r}$,可确定运动的加速度之比.
带电粒子运行的周期T=$\frac{2πm}{Bq}$,根据圆心角求出运行时间t=$\frac{θ}{2π}$T.从而求出运动时间之比.
解答 解:设磁场边长为a,如图所示,粒子从c点离开,其半径为rc,粒子从d点离开,其半径为rd;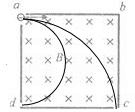
由Bqv=m$\frac{{v}^{2}}{r}$,得出半径公式r=$\frac{mv}{Bq}$,
又由运动轨迹知 rc=2rd 则vc:vd=2:1;
由T=$\frac{2πm}{Bq}$,根据圆心角求出运行时间t=$\frac{θ}{2π}$T.
运行时间 td=$\frac{T}{2}$,tc=$\frac{T}{4}$.则tc:td=1:2.
根据${a}_{n}=\frac{{v}^{2}}{r}$,可得ac:ad=2:1;
故选:AD
点评 本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.掌握带电粒子在匀强磁场中做匀速圆周运动的半径公式r=$\frac{mv}{Bq}$,和周期公式T=$\frac{2πm}{Bq}$.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
7.已知氢原子的基态能量为E1,激发态能量En=$\frac{{E}_{1}}{{n}^{2}}$,其中n=2,3….用h表示普朗克常量,c表示真空中的光速.能使氢原子从第一激发态电离的光子的最大波长为( )
| A. | -$\frac{4hc}{2{E}_{1}}$ | B. | -$\frac{2hc}{{E}_{1}}$ | C. | -$\frac{4hc}{{E}_{1}}$ | D. | -$\frac{9hc}{{E}_{1}}$ |
5. 观察水沸腾的过程中,水沸腾前和沸腾时水中气泡的上升情况如图甲、乙所示.关于这种现象的原因分析,下列说法中正确的是( )
观察水沸腾的过程中,水沸腾前和沸腾时水中气泡的上升情况如图甲、乙所示.关于这种现象的原因分析,下列说法中正确的是( )
 观察水沸腾的过程中,水沸腾前和沸腾时水中气泡的上升情况如图甲、乙所示.关于这种现象的原因分析,下列说法中正确的是( )
观察水沸腾的过程中,水沸腾前和沸腾时水中气泡的上升情况如图甲、乙所示.关于这种现象的原因分析,下列说法中正确的是( )| A. | 图甲中气泡在上升过程中泡内气体内能增大 | |
| B. | 图甲中气泡在上升过程中泡内气体释放热量 | |
| C. | 图甲中气泡在上升过程中泡内气体对外做功 | |
| D. | 图乙中气泡气体在上升过程中泡内气体内能增大 |
6. 如图所示,细线拴一带负电的小球,球处在竖直向下的匀强电场中,使小球在竖直平面内做圆周运动,则( )
如图所示,细线拴一带负电的小球,球处在竖直向下的匀强电场中,使小球在竖直平面内做圆周运动,则( )
 如图所示,细线拴一带负电的小球,球处在竖直向下的匀强电场中,使小球在竖直平面内做圆周运动,则( )
如图所示,细线拴一带负电的小球,球处在竖直向下的匀强电场中,使小球在竖直平面内做圆周运动,则( )| A. | 小球不可能做匀速圆周运动 | |
| B. | 小球运动到最低点时,球的线速度一定最大 | |
| C. | 小球运动到最低点时,电势能一定最大 | |
| D. | 当小球运动到最高点时绳的张力一定最小 |
 、
、 表示,则( )
表示,则( )
 B.
B.  、
、
 、
、 D.
D. 
 如图所示,在xOy坐标系第二象限内有一圆形匀强磁场区域,半径为,圆心O′坐标为(-l0,l0),磁场方向垂直xOy平面.在x轴上有坐标(-l0,0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴正方向,b的入射方向与y轴正方向夹角为θ=$\frac{π}{3}$.电子a经过磁场偏转后从y轴上的Q(0,l0)点进人第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求:
如图所示,在xOy坐标系第二象限内有一圆形匀强磁场区域,半径为,圆心O′坐标为(-l0,l0),磁场方向垂直xOy平面.在x轴上有坐标(-l0,0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴正方向,b的入射方向与y轴正方向夹角为θ=$\frac{π}{3}$.电子a经过磁场偏转后从y轴上的Q(0,l0)点进人第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求: 如图所示,一个重为10牛顿的L形均匀直角支架放在地面上,AO端长0.8米,BO端长1.2米,将重为30牛顿、半径为0.2米的光滑小球用长0.2米绳悬挂在A端,若支架不倾倒,则应在B端至少加力2牛,若将绳子缩短一些,则该力应变大(填:“变大”、“不变”或“变小”)
如图所示,一个重为10牛顿的L形均匀直角支架放在地面上,AO端长0.8米,BO端长1.2米,将重为30牛顿、半径为0.2米的光滑小球用长0.2米绳悬挂在A端,若支架不倾倒,则应在B端至少加力2牛,若将绳子缩短一些,则该力应变大(填:“变大”、“不变”或“变小”)