题目内容
13.在所有能源中,核能具有能量密度大、区域适应性强的优势.在核电站中,核反应堆释放的核能被转化为电能.核反应堆的工作原理是利用中子轰击重核发生裂变反应,释放出大量的核能.(1)核反应方程${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+aX是反应堆中发生的许多核反应中的一种,则a的值为多少,X表示哪一种核?
(2)上述反应中,分别用mU、mB、mK表示${\;}_{92}^{235}$U、${\;}_{56}^{141}$Ba、${\;}_{36}^{92}$Kr的质量,用mn和mp表示中子和质子的质量,则该反应过程中释放的核能为多少?
(3)有一座核能发电站,发电能力P=1×106kW,核能转化为电能的效率η=45%,设反应堆中发生的裂变反应全是(1)中的核反应,已知每次核反应过程中放出的核能E1=2.78×10-11J,铀核的质量mU=3.9×10-25kg,求每年(365天)需要消耗的铀的质量.(结果保留2位有效数字)
分析 根据电荷数守恒、质量数守恒得出aX的电荷数和质量数,从而确定a的个数和X为何种粒子.根据爱因斯坦质能方程求出释放的核能.
解答 解:(1)根据质量数和核电荷数守恒可得:
知aX的电荷数为0,质量数为3,知X的电荷数为0,质量数为1,X为中子,a=3.
(2)反应过程中质量亏损为△m=mU-mB-mK-2mn,
根据质能方程:E=△mC2,
可得该反应过程中释放的核能:
E=(mU-mB-mK-2mn)c2;
(3)该核能发电站一年发出的电能为:W1=Pt=1×109×365×24×3600J=3.1536×1016J
需要核反应产生的能量为:W=$\frac{{W}_{1}}{η}$=7.008×1016J
这么多核能需要燃烧的铀核质量为m=$\frac{W}{2.78×1{0}^{-11}}$mU
代入数据,解得:m=980kg=0.98t
答:(1)则a的值为3,X表示中子;
(2)则该反应过程中释放的核能为(mU-mB-mK-2mn)c2;
(3)每年(365天)需要消耗的铀的质量0.98t.
点评 本题考查了核反应方程和爱因斯坦质能方程的基本运用,比较简单,要加强训练,才能熟练.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
3. 如图a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星;a、b质量相同,且小于c的质量,则( )
如图a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星;a、b质量相同,且小于c的质量,则( )
 如图a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星;a、b质量相同,且小于c的质量,则( )
如图a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星;a、b质量相同,且小于c的质量,则( )| A. | b、c周期相同且大于a的周期 | B. | b、c的线速度相等且大于a的线速度 | ||
| C. | c所受地球的万有引力大于b | D. | a、c的向心加速度相等 |
4. 如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )
如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )
 如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )
如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )| A. | va:vb:vc:vd=2:1:2:6 | B. | ωa:ωb:ωc:ωd=2:1:1:1 | ||
| C. | aa:ab:ac:ad=4:1:2:4 | D. | aa:ab:ac:ad=4:1:2:6 |
8. 如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )
如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )
 如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )
如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )| A. | 玻璃砖对a光的折射率小于对b光的折射率 | |
| B. | 在玻璃中,a光的传播速度大于b光的传播速度 | |
| C. | 在真空中,a光的传播速度小于b光的传播速度 | |
| D. | 若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失 |
18.如图所示的电路中,如果交变电流的频率增大,1、2和3灯的亮度变化情况是( )


| A. | 1灯变暗,2灯变亮,3灯亮度不变 | B. | 1灯变亮,2、3两灯均变暗 | ||
| C. | 1、2灯均变暗,3灯亮度不变 | D. | 1、2两灯均变亮,3灯变暗 |
5.一半径为R、质量可视为均匀分布的球形行星的密度为ρ,自转周期为T0,若万有引力常量为G,则( )
| A. | 该行星表面重力加速度在两极的大小为$\frac{4}{3}$GρRπ | |
| B. | 该行星的卫星在星球表面附近做圆周运动的速率为2πR$\sqrt{\frac{3π}{ρG}}$ | |
| C. | 该行星的同步卫星的轨道半径为R($\frac{ρG{T}_{0}^{2}}{3π}$)${\;}^{\frac{1}{3}}$ | |
| D. | 该行星的同步卫星的运行速率为$\frac{2πR}{{T}_{0}}$ |
2. 如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )
如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )
 如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )
如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )| A. | 折射光斑在弧形屏上沿C→F→B方向移动 | |
| B. | 折射光斑的亮度逐渐变暗 | |
| C. | 折射角一定大于反射角 | |
| D. | 反射光线转过的角度为θ | |
| E. | 当玻璃砖转至θ=45°时,恰好看不到折射光线.则此玻璃砖的折射率n=$\sqrt{2}$ |
 如图所示,某同学在研究平抛运动的实验中,在小方格纸上画出小球做平抛运动的轨迹以后,又在轨迹上取出a、b、c、d四个点(轨迹已擦去).已知小方格纸的边长L=1.6cm,g取10m/s2.请你根据小方格纸上的信息,通过分析计算完成下面几个问题:
如图所示,某同学在研究平抛运动的实验中,在小方格纸上画出小球做平抛运动的轨迹以后,又在轨迹上取出a、b、c、d四个点(轨迹已擦去).已知小方格纸的边长L=1.6cm,g取10m/s2.请你根据小方格纸上的信息,通过分析计算完成下面几个问题: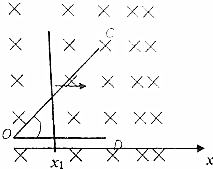 如图.水平面内有一“∠”型光滑金属导轨COD,电阻不计,∠COD=45°.足够长直导体棒搁在导轨上,单位长度的电阻为r=0.5Ω,导体棒垂直OD.空间存在垂直于导轨平面的磁场,以O点为原点沿0D方向建立坐标轴,导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,变化率为0.5T/m,O点磁感应强度B0=1T.在外力作用下,棒以一定的初速度向右做直线运动,运动时回路中的电流强度保持不变.已知运动到图中x1=1m位置时,速度大小v1=2m/s,则回路中的电流强度大小为6A,从x1=1m位置再向右运动1m的过程中,通过导体棒的电量为3.5C.
如图.水平面内有一“∠”型光滑金属导轨COD,电阻不计,∠COD=45°.足够长直导体棒搁在导轨上,单位长度的电阻为r=0.5Ω,导体棒垂直OD.空间存在垂直于导轨平面的磁场,以O点为原点沿0D方向建立坐标轴,导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,变化率为0.5T/m,O点磁感应强度B0=1T.在外力作用下,棒以一定的初速度向右做直线运动,运动时回路中的电流强度保持不变.已知运动到图中x1=1m位置时,速度大小v1=2m/s,则回路中的电流强度大小为6A,从x1=1m位置再向右运动1m的过程中,通过导体棒的电量为3.5C.