��Ŀ����
2�� ��ͼ��ʾ����Բ�β���ש��ͼ��ʵ��λ�÷��ã�ֱ����BD�غϣ�һ���������Ű�Բ�β���ש�İ뾶��Բ���洹ֱBD�䵽Բ��O���ϣ�ʹ����ש��O����ʱ�뻺����ת���ǶȦȣ�0�㣼�ȣ�90�㣩���۲쵽�����ߺͷ������ڻ��������ƶ����ڲ���שת�������У�����˵����ȷ���ǣ�������
��ͼ��ʾ����Բ�β���ש��ͼ��ʵ��λ�÷��ã�ֱ����BD�غϣ�һ���������Ű�Բ�β���ש�İ뾶��Բ���洹ֱBD�䵽Բ��O���ϣ�ʹ����ש��O����ʱ�뻺����ת���ǶȦȣ�0�㣼�ȣ�90�㣩���۲쵽�����ߺͷ������ڻ��������ƶ����ڲ���שת�������У�����˵����ȷ���ǣ�������| A�� | �������ڻ���������C��F��B�����ƶ� | |
| B�� | �����ߵ������䰵 | |
| C�� | �����һ�����ڷ���� | |
| D�� | �������ת���ĽǶ�Ϊ�� | |
| E�� | ������שת����=45��ʱ��ǡ�ÿ�����������ߣ���˲���ש��������n=$\sqrt{2}$ |
���� ����ש��O����ʱ�뻺����ת���ǶȦȵĹ����У���������������Ҳ��֮��������������������ͬ������ת��������������������ǿ���������������������ת��2�ȣ����ٽ�ǹ�ʽsinC=$\frac{1}{n}$����ٽ�ǣ�������שת����=45��ʱ��ǡ�ÿ�����������ߣ�ǡ�÷�����ȫ���䣬��ʱ������ǵ����ٽ�ǣ�
��� �⣺A������ש��O����ʱ�뻺����ת���ǶȦȵĹ����У���������������䶨��n=$\frac{sini}{sinr}$��֪�����Ҳ��֮�����ҷ���Ҳ��ʱ����ת�������������ڻ���������C��D�����ƶ�����A����
B��������������������ǿ���������������������ߵ������䰵����B��ȷ��
C������0�㣼�ȣ�90�㼰���䶨�ɿ�֪���ڲ���שת�������У������һ����������ǣ�������ǵ�������ǣ��������һ�����ڷ���ǣ���C��ȷ��
D�����ݷ��䶨�ɺͼ���֪ʶ֪������שת���Ƚǣ��������ת��2�Ƚǣ���D����
E��������שת����=45��ʱ��ǡ�ÿ�����������ߣ�ǡ�÷�����ȫ���䣬���ٽ��C=45�㣬���ٽ�ǹ�ʽsin C=$\frac{1}{n}$�����������n=$\sqrt{2}$����E��ȷ��
��ѡ��BCE
���� ���⿼������䶨�ɡ����䶨�ɵ�����������Ҫ֪������ӹ��ܽ��ʽ�������������ʱ�������С������ǣ���������ǵ����������ǿ����������������������������ͬ����ת��

| A�� | Ǧ�����ܵ�����̫�� | |
| B�� | Ǧ��Ĺ��Բ����� | |
| C�� | С����Ǧ���ٶ�̫С | |
| D�� | Ǧ�������������ٶȷ�����ͬһֱ���� |
 ����ͼ��ʾ�ĵ�·�У�L1��L2��������ͬ��С���ݣ�A��B�������߿��ڸ�����һ����ѧԪ����a��b���˷ֱ���ֱ����Դ�ͽ�����Դ�����ӣ���ֱ����Դ�ĵ�ѹ�뽻����Դ��ѹ����Чֵ��ȣ��۲���������µ��ݵ����ȣ�����ֱ����Դʱ��L1�����⣬L2�������⣻���ӽ�����Դʱ��L1���⣬L2���Ա䰵��������˵����ȷ���ǣ�������
����ͼ��ʾ�ĵ�·�У�L1��L2��������ͬ��С���ݣ�A��B�������߿��ڸ�����һ����ѧԪ����a��b���˷ֱ���ֱ����Դ�ͽ�����Դ�����ӣ���ֱ����Դ�ĵ�ѹ�뽻����Դ��ѹ����Чֵ��ȣ��۲���������µ��ݵ����ȣ�����ֱ����Դʱ��L1�����⣬L2�������⣻���ӽ�����Դʱ��L1���⣬L2���Ա䰵��������˵����ȷ���ǣ�������| A�� | A�нӵ��ǵ��裬B�нӵ��ǵ����� | |
| B�� | A�нӵ��ǵ�������B�нӵ��ǵ����Ȧ | |
| C�� | A�нӵ��ǵ����Ȧ��B�нӵ��ǵ����� | |
| D�� | A�нӵ��ǵ����Ȧ��B�нӵ��ǵ��� |
| A�� | ������A������������������A����ʾB�ĺ��� | |
| B�� | ������A����������Ҳ�ܿ���A����ʾB�ĺ���13022222222 | |
| C�� | �Ȳ�������A����������Ҳ������A����ʾB�ĺ��� | |
| D�� | ��������A�������������ܿ���A����ʾB�ĺ���13022222222 |
 �����ڹ�������������ʻ���������ɹ��ŵ���ߵ�A��ʻ����͵�B�Ĺ����У�����˵������ȷ���ǣ�������
�����ڹ�������������ʻ���������ɹ��ŵ���ߵ�A��ʻ����͵�B�Ĺ����У�����˵������ȷ���ǣ�������| A�� | ֧���������� | B�� | ���������� | C�� | Ħ���������� | D�� | ǣ���������� |
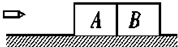 ��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ����������Ӵ���ľ��A��B�������ֱ�Ϊm 1��m 2������һ�ӵ�ˮƽ������ľ�飮���ӵ�����ľ��A��B��ʱ��ֱ�Ϊt1��t2��ľ����ӵ���������Ϊf�����ӵ�������ľ���ľ��A��B���ٶȴ�С�ֱ��ǣ�������
��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ����������Ӵ���ľ��A��B�������ֱ�Ϊm 1��m 2������һ�ӵ�ˮƽ������ľ�飮���ӵ�����ľ��A��B��ʱ��ֱ�Ϊt1��t2��ľ����ӵ���������Ϊf�����ӵ�������ľ���ľ��A��B���ٶȴ�С�ֱ��ǣ�������| A�� | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ | |
| B�� | $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$ $\frac{f{t}_{1}}{{m}_{1}+{m}_{2}}$+$\frac{f{t}_{2}}{{m}_{2}}$ | |
| C�� | $\frac{f{t}_{1}}{{m}_{1}}$ $\frac{f��{t}_{1}+{t}_{2}��}{{m}_{1}+{m}_{2}}$ | |
| D�� | $\frac{f��{t}_{1}+{t}_{2}��}{{m}_{1}}$ $\frac{f��{t}_{1}+{t}_{2}��}{{m}_{1}+{m}_{2}}$ |

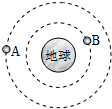 ��ͼ��ʾ����������A��B��ͬһƽ�����Ƶ���������Բ���˶���������A�����ٶ�С������B�����ٶȣ�����A�ļ��ٶ�С������B�ļ��ٶȣ�ѡ����ڡ�����С�ڡ����ڡ�����
��ͼ��ʾ����������A��B��ͬһƽ�����Ƶ���������Բ���˶���������A�����ٶ�С������B�����ٶȣ�����A�ļ��ٶ�С������B�ļ��ٶȣ�ѡ����ڡ�����С�ڡ����ڡ�����