题目内容
16.如图所示,一小车上表面由粗糙的水平部分AB和光滑的半圆弧轨道BCD组成,小车紧靠台阶静止在光滑水平地面上,且左端与粗糙水平台等高.水平台与物块P间的滑动摩擦因数为μ=0.2,水平台上有一弹簧,弹簧左端固定,弹簧右端与一个质量为m1=5kg的小物块接触但不固定,此时弹簧处于压缩状态并锁定,弹簧的弹性势能EP=100J.现解除弹簧的锁定,小物块P从M点出发,MN间的距离为d=lm.物块P到N点后与静止在小车左端的质量为m2=lkg的小物块Q(可视为质点)发生弹性碰撞(碰后立即将小物块P取走,使之不影响后续物体的运动).已知AB长为L=10m,小车的质量为M=3kg.取重力加速度g=10m/s2,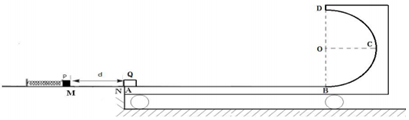
(1)求碰撞后瞬间物块Q的速度大小,
(2)若物块Q在半圆弧轨道BCD上经过一次往返运动(运动过程中物块始终不脱离轨道),最终停在小车水平部分AB的中点,求半圆弧轨道BCD的半径至少多大?
(3)若小车上表面AB和半圆弧轨道BCD面均光滑,半圆弧轨道BCD的半径为R=1.2m,物块Q可以从半圆弧轨道BCD的最高点D飞出,求其再次落回小车时,落点与B点的距离S为多少?(结果可用根号表示)
分析 (1)根据能量守恒求出物块P被弹簧弹开后的速度,物块P、Q发生弹性碰撞,结合动量守恒和机械能守恒求出碰撞后瞬间物块Q的速度大小.
(2)物块Q和小车组成的系统在水平方向上动量守恒,结合动量守恒定律求出共同的速度,根据能量守恒求出物块Q与小车间的动摩擦因数大小,对物块Q到达圆弧的最高点过程,运用能量守恒求出半径的临界值.
(3)根据动量守恒能量守恒求出Q通过D点时,Q的速度和哀愁的速度,结合平抛运动的规律,抓住物块相对D点的速度,求出落点与B点的距离.
解答 解:(1)物块P被弹簧弹开运动到N点速度为v1,由能量守恒得:
${E}_{p}=μmgd+\frac{1}{2}m{{v}_{1}}^{2}$
代入数据解得v1=6m/s.
物块P、Q发生弹性碰撞,碰后P、Q的速度为v1'、v2,规定向右为正方向,
m1v1=m1v1′+m2v2,
$\frac{1}{2}{m}_{1}{{v}_{1}}^{2}=\frac{1}{2}{m}_{1}{v}_{1}{′}^{2}+\frac{1}{2}{m}_{2}{{v}_{2}}^{2}$
代入数据解得:v1'=4m/s,v2=10 m/s或v1'=6m/s,v2=0 (舍).
(2)物块Q从开始运动到与小车相对静止过程,共同速度为v3,系统动量守恒,规定向右为正方向,有:
m2v2=(m2+M)v3,
代入数据解得:v3=2.5m/s,
系统能量守恒:$\frac{1}{2}{m}_{2}{{v}_{2}}^{2}=μ{m}_{2}g•\frac{3}{2}L+\frac{1}{2}({m}_{2}+M){{v}_{3}}^{2}$,
代入数据解得:μ=0.25.
Q至C点与车共速时,半径R最小,系统能量守恒,有:$\frac{1}{2}{m}_{2}{{v}_{2}}^{2}=μ{m}_{2}gL+{m}_{2}gR$$+\frac{1}{2}({m}_{2}+M){{v}_{3}}^{2}$,
代入数据解得:R=1.25m.
(3)设Q通过D点时,Q与小车的速度分别为v4、v5系统动量、能量守恒,规定向右为正方向,
m2v2=m2v4+Mv5,
$\frac{1}{2}{m}_{2}{{v}_{2}}^{2}=\frac{1}{2}{m}_{2}{{v}_{4}}^{2}+\frac{1}{2}M{{v}_{5}}^{2}+$m2g•2R
解得:v4=-2m/s,v5=4 m/s或v4=7m/s,v5=1 m/s(舍)
物块Q通过D点时相对小车的速度为:v4′=6 m/s,
物块Q再次落回小车时与物块的距离为:s=${v}_{4}′\sqrt{\frac{4R}{g}}$,
代入数据解得:s=$\sqrt{\frac{12\sqrt{3}}{5}}m$.
答:(1)碰撞后瞬间物块Q的速度大小为10m/s.
(2)半圆弧轨道BCD的半径至少为1.25m.
(3)落点与B点的距离S为$\sqrt{\frac{12\sqrt{3}}{5}}m$.
点评 本题考查了动量守恒、能量守恒的综合运用,涉及到圆周运动、平抛运动的知识,知道弹性碰撞的过程中,动量守恒、机械能守恒,对于第二问,要抓住临界情况,即到达圆弧最高点两者具有相同速度,结合能量守恒进行求解.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案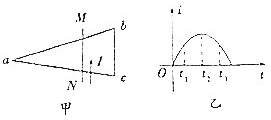 等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )| A. | 在任何时刻线框中都无感应电流 | |
| B. | 在t1时刻线框中有沿acba方向的感应电流 | |
| C. | 在t2时刻线框中有沿acba方向的感应电流 | |
| D. | 在t3时刻线框中有沿abca方向的感应电流 |
| A. | 10N | B. | 15N | C. | 20N | D. | 25N |
 如图所示,物体A和B质量均为m,且分别与轻绳连结跨过光滑轻质定滑轮,当用力F拉B沿水平面向右匀速运动过程中,绳对A的拉力的大小是( )
如图所示,物体A和B质量均为m,且分别与轻绳连结跨过光滑轻质定滑轮,当用力F拉B沿水平面向右匀速运动过程中,绳对A的拉力的大小是( )| A. | 大于mg | B. | 等于F | C. | 总等于mg | D. | 小于mg |
 如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )
如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )| A. | 小球在tB时刻所受弹簧弹力等于0.5mg | |
| B. | 整个过程小球的机械能守恒 | |
| C. | 小球从tC时刻所在的位置由静止释放后,不能回到出发点 | |
| D. | 小球从tA时刻到tC时刻的过程中重力势能的减少量小于弹簧弹性势能的增加量 |
 如图所示,倾角为θ 的绝缘斜面上有一质量(全部集中在cd边,其他边质量不计)为m的正方形线圈,线圈的边长为L,每条边的电阻均为R.ABCD是矩形匀强磁场区域,磁感应强度大小为B,磁场的方向垂直于斜面向上(图中未画出).AB和CD之间的距离为L,CD和PQ之间的距离 为2.5L.CD上方斜面是光滑的,CD下方斜面是粗糙的,且线圈与斜面间的动摩擦因数为μ.线圈abcd从图示位置由静止开始下滑,cd边进入磁场时线框所受合力恰好为0,重力加速度为g.
如图所示,倾角为θ 的绝缘斜面上有一质量(全部集中在cd边,其他边质量不计)为m的正方形线圈,线圈的边长为L,每条边的电阻均为R.ABCD是矩形匀强磁场区域,磁感应强度大小为B,磁场的方向垂直于斜面向上(图中未画出).AB和CD之间的距离为L,CD和PQ之间的距离 为2.5L.CD上方斜面是光滑的,CD下方斜面是粗糙的,且线圈与斜面间的动摩擦因数为μ.线圈abcd从图示位置由静止开始下滑,cd边进入磁场时线框所受合力恰好为0,重力加速度为g. 如图所示的图象表示的是位移-时间图象.AB段表示物体处于静止状态.BC段表示物体做匀速直线运动,其运动方向与选定的正方向相同.CD段表示物体做匀速直线运动,其运动方向与选定的正方向相反.
如图所示的图象表示的是位移-时间图象.AB段表示物体处于静止状态.BC段表示物体做匀速直线运动,其运动方向与选定的正方向相同.CD段表示物体做匀速直线运动,其运动方向与选定的正方向相反.


