题目内容
13. 在电场强度为E=104N/C、方向水平向右的匀强电场中,用一根长L=1m的绝缘细杆(质量不计)固定一个质量为m=0.2kg的电量为q=5×10-6C带正电的小球,细杆可绕轴O在竖直平面内自由转动.现将杆从水平位置A轻轻释放,在小球运动到最低点B的过程中:取g=10m/s2,求:
在电场强度为E=104N/C、方向水平向右的匀强电场中,用一根长L=1m的绝缘细杆(质量不计)固定一个质量为m=0.2kg的电量为q=5×10-6C带正电的小球,细杆可绕轴O在竖直平面内自由转动.现将杆从水平位置A轻轻释放,在小球运动到最低点B的过程中:取g=10m/s2,求:(1)小球到达B点时的速度多大?
(2)小球到达B点时,杆对小球的作用力大小?
分析 (1)根据动能定理求出小球到达B点时的速度大小.
(2)根据牛顿第二定律,结合竖直方向上的合力提供向心力求出杆对小球的作用力大小.
解答 解:(1)根据动能定理得:$mgL+qEL=\frac{1}{2}m{v}^{2}$,
解得:v=$\sqrt{\frac{2(mg+qE)L}{m}}$=$\sqrt{\frac{2×(2+5×1{0}^{-6}×1{0}^{4})×1}{0.2}}$m/s=4.5m/s.
(2)根据牛顿第二定律得:F-mg=m$\frac{{v}^{2}}{L}$,
解得:F=mg+$m\frac{{v}^{2}}{L}$=$2+0.2×\frac{20.5}{1}$N=6.1N.
答:(1)小球到达B点的速度为4.5m/s.
(2)小球到达B点时,杆对小球的作用力大小为6.1N.
点评 本题考查了牛顿第二定律和动能定理的综合运用,知道小球在最低点向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
4.如图所示,为A、B两物体从同一地点沿同一方向做直线运动的速度-时间图象.由图可知( )

| A. | A出发时间比B出发晚5s | |
| B. | 10s末A、B速度相等,此时两者相距75m(追上前最远) | |
| C. | 在15s末A追上了B | |
| D. | 在图示中的15s内A没能追上B,但由图可以推算出:在t≈18.66s时A追上了B |
18.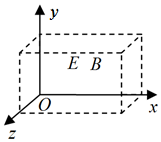 在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )
在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )
 在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )
在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )| A. | E和B都沿x轴方向 | B. | E沿y轴正向,B沿z轴正向 | ||
| C. | E沿z轴正向,B沿y轴正向 | D. | E沿z轴正向,B沿y轴负向 |
5.一个物体放在斜面上,当斜面的倾角逐渐增大而物体仍静止在斜面上时,下列说法正确的是( )
| A. | 重力与支持力的合力逐渐增大 | B. | 重力与静摩擦力的合力逐渐增大 | ||
| C. | 支持力与静摩擦力的合力逐渐增大 | D. | 重力、支持力、静摩擦力的合力不变 |
2.下列有关电场线的说法中,正确的是( )
| A. | 电场线的疏密程度表示电场的强弱 | |
| B. | 同一电场中任意两条电场线不相交 | |
| C. | 电场线上某点的切线方向就是放在该点的点电荷所受电场力的方向 | |
| D. | 带电粒子在只受电场力时,运动轨迹一定与电场线重合 |
 如图所示,皮带轮带动传送带沿逆时针方向以速度v0=2m/s匀速运动,两皮带轮之间的距离L=3.2m,皮带绷紧与水平方向的夹角θ=37°.将一可视为质点的小物块无初速地从上端放到传送带上,已知物块与传送带间的动摩擦因数μ=0.5(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
如图所示,皮带轮带动传送带沿逆时针方向以速度v0=2m/s匀速运动,两皮带轮之间的距离L=3.2m,皮带绷紧与水平方向的夹角θ=37°.将一可视为质点的小物块无初速地从上端放到传送带上,已知物块与传送带间的动摩擦因数μ=0.5(sin37°=0.6,cos37°=0.8,取g=10m/s2)求: 如图所示,A为粒子源.在A和极板B间的加速电压为U1,在两水平放置的平行导体板C、D间加有偏转电压U2.C、D板长L,板间距离d.现从粒子源A发出质量为m,带电量为q的带电粒子,由静止开始经加速电场加速后进入偏转电场,最后穿出打在右侧的屏幕上,不计粒子的重力.求:
如图所示,A为粒子源.在A和极板B间的加速电压为U1,在两水平放置的平行导体板C、D间加有偏转电压U2.C、D板长L,板间距离d.现从粒子源A发出质量为m,带电量为q的带电粒子,由静止开始经加速电场加速后进入偏转电场,最后穿出打在右侧的屏幕上,不计粒子的重力.求:
