��Ŀ����
16��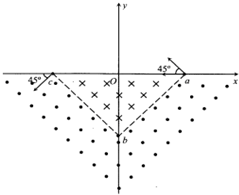 ��ͼ��ʾ��ƽ��ֱ������ϵ�У�a��b��c���������ֱ�Ϊa��L��0����b��0��-L����c��-L��0������abc�����ڣ����߽磩���ڷ���ֱ��xOyƽ���������ǿ�ų�����abc�⣬��y��0�������ڴ��ڷ���ֱ��xOyƽ���������ǿ�ų������ų�����ĴŸ�Ӧǿ�ȴ�С��ȣ���y��0�������ڻ�����һ���Ÿ�Ӧǿ�ȴ�СΪB������ֱ��xOyƽ��ľ�����ǿ�ų�����ͼ��δ�����������εױ�ƽ����x�ᡢ�Խ��ߵĽ�����y���ϣ�������������Ϊ�ʵ㣬������Ϊm���������Ϊq�Ĵ���������ͬʱ��a����������Ӽij��ٶȷ�����x�Ḻ�����45��ǣ������ҵij��ٶȷ�����x�Ḻ��������a��b����c��ʱ���պ��������������ʱ���ٶȷ���Ҳ��x�Ḻ�����45��ǣ�����֪���Ӽ��ڵ�1������ֱ���˶���ʱ��������ھ��������ڵ��˶�ʱ�䣬�ռ�Ϊ��գ������������������Ӽ��������������������˶��Ե硢�ų�������Ӱ�죮
��ͼ��ʾ��ƽ��ֱ������ϵ�У�a��b��c���������ֱ�Ϊa��L��0����b��0��-L����c��-L��0������abc�����ڣ����߽磩���ڷ���ֱ��xOyƽ���������ǿ�ų�����abc�⣬��y��0�������ڴ��ڷ���ֱ��xOyƽ���������ǿ�ų������ų�����ĴŸ�Ӧǿ�ȴ�С��ȣ���y��0�������ڻ�����һ���Ÿ�Ӧǿ�ȴ�СΪB������ֱ��xOyƽ��ľ�����ǿ�ų�����ͼ��δ�����������εױ�ƽ����x�ᡢ�Խ��ߵĽ�����y���ϣ�������������Ϊ�ʵ㣬������Ϊm���������Ϊq�Ĵ���������ͬʱ��a����������Ӽij��ٶȷ�����x�Ḻ�����45��ǣ������ҵij��ٶȷ�����x�Ḻ��������a��b����c��ʱ���պ��������������ʱ���ٶȷ���Ҳ��x�Ḻ�����45��ǣ�����֪���Ӽ��ڵ�1������ֱ���˶���ʱ��������ھ��������ڵ��˶�ʱ�䣬�ռ�Ϊ��գ������������������Ӽ��������������������˶��Ե硢�ų�������Ӱ�죮��1��ָ�����������ڴų��ķ�������ھ������������е�ʱ��t��������v����
��2�����ҵ�����v����y��0�����ڵĴŸ�Ӧǿ�ȴ�СB�������������
���� ����һ�����ӵĴų�����Ĵ������ӵ��˶��ۺϣ������ų������������ӴӲ�ͬ�����ز�ͬ���˶�·�����ﵽͬһ�㣮Ҫ���Ǻܶ�Գ��������ԣ�
��1�������������Ӵ�a��c���������Σ������ֶ�������жϾ��δų������ڵķ������������и��������Ӽ��ڵ�1������ֱ���˶���ʱ��������ھ��������ڵ��˶�ʱ�䣬�ɼ��ι�ϵ�ʹ���������������ھ������������е�ʱ��t�������ʣ�
��1�������������ִų���������Բ���˶�������Ƚϸ��ӣ���a������Ⱥ�������������������Բ���˶��������Ҫ�ﵽc�㣬�ɼ��ι�ϵ����뾶��L�Ĺ�ϵ����Ҫ������������п��ǣ�������a��b�������Σ����ܻ���Ϊs1=n��2��R��=2��L���Ӷ������������������ӵ��ٶȣ�������a��b��ż���Σ����ܻ���${s}_{2}=\frac{n}{2}��2��R��=��L$
��������֪��ʱ�������������������ҵ��ٶȣ����ɰ뾶��ʽ����Ÿ�Ӧǿ�ȣ�
��� �⣺��1�����ھ���������������ֱ���˶����ھ���������������Բ���˶����������������˶��켣��ͼ��ʾ��
�����ֶ���ɵôų�����Ϊ��ֱ��xoyƽ������
�ڴų��У���ƫת�ĽǶ�Ϊ90��
��ţ�ٵڶ����ɶ����У�$q{v}_{��}B=\frac{m{{v}_{��}}^{2}}{R}$ 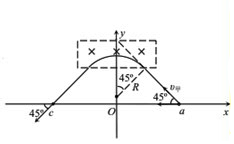
�ɵð뾶��$R=\frac{m{v}_{��}}{qB}$�����ڣ�$T=\frac{2��m}{qB}$
�˶�ʱ�䣺$t=\frac{90��}{360��}T=\frac{��m}{2qB}$
�ɼ��ι�ϵ�ɵü��ڵڢ�������ֱ���˶���λ��Ϊ��$x=\frac{L}{cos45��}-Rtan45��$
�ڵڢ�������ֱ���˶���ʱ�䣺$t=\frac{x}{{v}_{��}}$
������ã�v��=$\frac{2\sqrt{2}qBL}{��2+�У�m}$
��2���������⣬����a��c������ʱ��Ϊ${t}_{��}=3t=\frac{3��m}{2qB}$
�����ڴų���������Բ���˶��Ĺ���뾶ΪR��
��ţ�ٵڶ������У�$q{v}_{��}B=\frac{m{{v}_{��}}^{2}}{R��}$
�����˶��ĶԳ��ԣ�����a��b����c���˶��켣��ͼ��ʾ������x����ÿ��Բ���켣��Ӧ���ҳ�����nΪ��a��b��Ӧ��Բ������
$\sqrt{2}L=nx��$
�ɼ��ι�ϵ�У�$\sqrt{2}R��=x��$
����������ʽ�ã�$R��=\frac{L}{n}$
�ٵ�nΪż��ʱ�����л������ܳ�Ϊs1=n��2��R��=2��L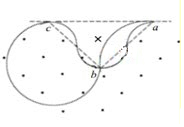
${v}_{��}=\frac{{s}_{1}}{{t}_{��}}=\frac{4qBL}{3m}$
$B��=\frac{m{v}_{��}}{qR��}=\frac{4}{3}nB$ ��n=1��3��5����
�ڵ�nΪż��ʱ�����л������ܳ�Ϊ${s}_{2}=\frac{n}{2}��2��R��=��L$
${v}_{��}=\frac{{s}_{2}}{{t}_{��}}=\frac{2qBL}{3m}$
$B��=\frac{m{v}_{��}}{qR��}=\frac{2}{3}nB$ ��n=2��4��6����
�𣺣�1�����������ڴų��ķ���Ϊ��ֱֽ��������ھ������������е�ʱ��t��������Ϊ$\frac{2\sqrt{2}qBL}{��2+�У�m}$��
��2���ҵ�����Ϊ${v}_{��}=\frac{{s}_{1}}{{t}_{��}}=\frac{4qBL}{3m}$ ��$B��=\frac{m{v}_{��}}{qR��}=\frac{4}{3}nB$ ��n=1��3��5���� ����${v}_{��}=\frac{{s}_{2}}{{t}_{��}}=\frac{2qBL}{3m}$ ��$B��=\frac{m{v}_{��}}{qR��}=\frac{2}{3}nB$ ��n=2��4��6������
���� ������������ڵ����ʣ����ڼ��������Ӵ�a��c��ʱ����ȣ�����ֻҪ����ҵ���·�̣��Ϳ�����������ӵ��ٶȣ����ɰ뾶��ʽ����Ÿ�Ӧǿ�ȵĴ�С���������ӵ��˶�����Ƚϸ��ӵ��ܾ��жԳ��ԣ�Ҫ��������ż������������ǣ�

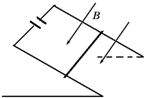
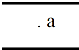 ��ͼ����ƽ�е��㹻����������ˮƽ���ã�������ǿ�糡�����������м�a��Ӿ�ֹ�ͷ�һ����������ǡ�ñ��־�ֹ״̬���ֽ������ƹ�a����ᣨ��ֱ��ֽ�棩˳ʱ����ת60�㣬����a��Ӿ�ֹ�ͷŸ�������������������
��ͼ����ƽ�е��㹻����������ˮƽ���ã�������ǿ�糡�����������м�a��Ӿ�ֹ�ͷ�һ����������ǡ�ñ��־�ֹ״̬���ֽ������ƹ�a����ᣨ��ֱ��ֽ�棩˳ʱ����ת60�㣬����a��Ӿ�ֹ�ͷŸ�������������������| A�� | ��ֱ���˶��������Ͻ��������� | B�� | ��ֱ���˶��������½��������� | ||
| C�� | �������˶��������Ͻ��������� | D�� | �������˶��������½��������� |
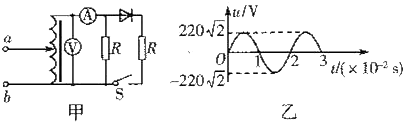 ��ͼ����ʾ�����������ѹ�������a��b����ͼ����ʾ�Ľ����磬һ����������ܣ��������Ϊ�㣬������������������ֵ��ΪR=40���ĸ��ص���ӵ�����Ȧ�����ˣ�����Ƭλ��ԭ��Ȧ�е�λ��ʱ������S���ڶϿ�״̬������˵����ȷ���ǣ�ͼ�е����Ϊ���뽻���������������
��ͼ����ʾ�����������ѹ�������a��b����ͼ����ʾ�Ľ����磬һ����������ܣ��������Ϊ�㣬������������������ֵ��ΪR=40���ĸ��ص���ӵ�����Ȧ�����ˣ�����Ƭλ��ԭ��Ȧ�е�λ��ʱ������S���ڶϿ�״̬������˵����ȷ���ǣ�ͼ�е����Ϊ���뽻���������������| A�� | t=0.01s�ԣ���ѹ��ʾ��Ϊ�� | B�� | t=0.015 sʱ��������ʾ��Ϊ11A | ||
| C�� | �պϿ���S��ѹ��ʾ������ | D�� | �պϿ���S������ʾ��Ϊl6.5 A |
| A�� | С�����ڿ�����ƽ���˶��Ĺ��� | B�� | �˳˵��ݼ��������Ĺ��� | ||
| C�� | ľ����б���������»��еĹ��� | D�� | ��ɡ�˶�Ա�ڿ�����������Ĺ��� |
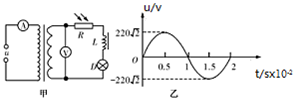 ��ͼ����ʾ�ĵ�·�У������ѹ��ԭ������Ȧ������Ϊ10��1��A��V��Ϊ��������R��L��D�ֱ��ǹ������裨����ֵ���ǿ�������С����������Ȧ�͵��ݣ�ԭ��Ȧ������ͼ����ʾ�����ҽ�����ѹu������˵����ȷ���ǣ�������
��ͼ����ʾ�ĵ�·�У������ѹ��ԭ������Ȧ������Ϊ10��1��A��V��Ϊ��������R��L��D�ֱ��ǹ������裨����ֵ���ǿ�������С����������Ȧ�͵��ݣ�ԭ��Ȧ������ͼ����ʾ�����ҽ�����ѹu������˵����ȷ���ǣ�������| A�� | ��ѹu��Ƶ��Ϊ100 Hz | B�� | V��ʾ��Ϊ22$\sqrt{2}$V | ||
| C�� | �й�����Rʱ��A��ʾ����� | D�� | ���L�е���о��D�䰵 |

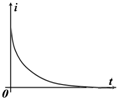
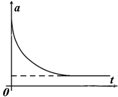
 ��ͼ�����㹻���Ĺ⻬ƽ�н���������б���ã�������˽�����ѹ�㹻�ĵ�����C����ǿ�ų�B��ֱ����ƽ�棬��һ�������ֱ����ʹų����ã��ɽ����������ɻ�����������͵��������Բ��ƣ��ֵ�����ɾ�ֹ�ͷţ����������˵�ѹΪU����������ٶ�Ϊa��ͨ���ĵ���Ϊi����������ΪP��������ͼ������ȷ��ӳ������ʱ��仯���ɵ��ǣ���������
��ͼ�����㹻���Ĺ⻬ƽ�н���������б���ã�������˽�����ѹ�㹻�ĵ�����C����ǿ�ų�B��ֱ����ƽ�棬��һ�������ֱ����ʹų����ã��ɽ����������ɻ�����������͵��������Բ��ƣ��ֵ�����ɾ�ֹ�ͷţ����������˵�ѹΪU����������ٶ�Ϊa��ͨ���ĵ���Ϊi����������ΪP��������ͼ������ȷ��ӳ������ʱ��仯���ɵ��ǣ���������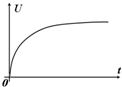

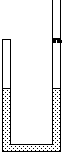 ��ͼ��ʾ����ֱ���õ�U�ιܵĺ�������ΪS����װ�ܶ�Ϊ�ѵ�Һ�壬��g=0.1atm/m���Ҳ���������ͨ���㹻�����ҹ�����һ����Ϊm�Ļ������ڹ̶������ϣ�����λ�����ҹ��϶˵ȸߣ���ʼʱ�����ҹ���Һ��߶���ȣ������ڿ��������Ⱦ�Ϊl0=1.0m��ѹǿ��Ϊ����ѹǿp0=1atm����ʹ��������������ͬ���¶ȣ�ƽ��ʱ������Һ���½�h=0.1m����ʱ�Ҳ�������峤��Ϊ1.12m������֪��mg/S=0.01atm��
��ͼ��ʾ����ֱ���õ�U�ιܵĺ�������ΪS����װ�ܶ�Ϊ�ѵ�Һ�壬��g=0.1atm/m���Ҳ���������ͨ���㹻�����ҹ�����һ����Ϊm�Ļ������ڹ̶������ϣ�����λ�����ҹ��϶˵ȸߣ���ʼʱ�����ҹ���Һ��߶���ȣ������ڿ��������Ⱦ�Ϊl0=1.0m��ѹǿ��Ϊ����ѹǿp0=1atm����ʹ��������������ͬ���¶ȣ�ƽ��ʱ������Һ���½�h=0.1m����ʱ�Ҳ�������峤��Ϊ1.12m������֪��mg/S=0.01atm��