题目内容
6. 带电粒子的质量m=1.7×10-27Kg,电量q=1.6×10-19C,以速度v=3.2×106m/s沿垂直于磁场同时又垂直于磁场边界的方向射入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度L=10cm,如图所示.不计粒子重力.求
带电粒子的质量m=1.7×10-27Kg,电量q=1.6×10-19C,以速度v=3.2×106m/s沿垂直于磁场同时又垂直于磁场边界的方向射入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度L=10cm,如图所示.不计粒子重力.求(1)带电粒子离开磁场时的速度多大?
(2)带电粒子在磁运动多长时间?
(3)带电粒子离开磁场时平行于磁场边界的位移大小?
分析 (1)带电粒子在匀强磁场中做匀速圆周运动,速率不变
(2)由洛伦兹力提供向心力求得周期公式,由运动径迹得到圆弧运动时间与周期的关系,进而求出时间
(3)分析轨迹特点,由几何关系得出偏离入射方向的距离
解答  解:(1)由于粒子在磁场中做匀速圆周运动,故粒子离开磁场时的速度大小为3.2×106m/s
解:(1)由于粒子在磁场中做匀速圆周运动,故粒子离开磁场时的速度大小为3.2×106m/s
(2)带电粒子在磁场中运动的时间为:$t=\frac{θ}{2π}T=\frac{30°}{360°}\frac{2πm}{qB}=3.3×{10^{-8}}s$
(3)由洛伦兹力提供向心力:qvB=m$\frac{v^2}{R}$
得R=20cm
由图知$sinθ=\frac{L}{R}=\frac{1}{2}$
即:带电粒子离开磁场时的偏转角为:θ=30°
平行于磁场边界的位移大小:$d=R-Rcos30°=20-10\sqrt{3}cm=2.7cm$
答:(1)带电粒子离开磁场时的速度$3.2×1{0}_{\;}^{6}m/s$
(2)带电粒子在磁运动时间$3.3×1{0}_{\;}^{-6}s$
(3)带电粒子离开磁场时平行于磁场边界的位移大小2.7cm
点评 本题考查带电粒子在磁场中的运动,重点是画出轨迹,分析轨迹中的几何关系,结合带带电粒子的半径和周期公式求解.

练习册系列答案
相关题目
14.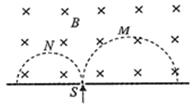 2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )
2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )
 2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )
2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )| A. | N为负电子,M为正电子 | B. | N的速率小于M的速率 | ||
| C. | 洛伦兹力对M做正功、对N做负功 | D. | M的运行时间大于N的运行时间 |
16. 某小孩在广场游玩时,将一氢气球系在了水平地面上的砖块上,在水平风力的作用下,处于如图所示的静止状态.若水平风速缓慢增大,不考虑气球体积及空气密度的变化,下列说法中正确的是( )
某小孩在广场游玩时,将一氢气球系在了水平地面上的砖块上,在水平风力的作用下,处于如图所示的静止状态.若水平风速缓慢增大,不考虑气球体积及空气密度的变化,下列说法中正确的是( )
 某小孩在广场游玩时,将一氢气球系在了水平地面上的砖块上,在水平风力的作用下,处于如图所示的静止状态.若水平风速缓慢增大,不考虑气球体积及空气密度的变化,下列说法中正确的是( )
某小孩在广场游玩时,将一氢气球系在了水平地面上的砖块上,在水平风力的作用下,处于如图所示的静止状态.若水平风速缓慢增大,不考虑气球体积及空气密度的变化,下列说法中正确的是( )| A. | 细绳受到的拉力逐渐减小 | B. | 砖块不可能被绳子拉离地面 | ||
| C. | 砖块受到的摩擦力一直增大 | D. | 砖块受到的摩擦力一直不变 |

 有一平行板电容器,内部为真空,两个电极板间的间距为$\frac{L}{2}$,极板长为L,极板间有一匀强电场,U为两极板间的电压,电子从极板左端的正中央以初速v0射入,其方向平行于极板,并打在极板上,如图(甲)所示.电子的电荷量用e表示,质量用m表示,重力不计.回答下面问题(用字母表示结果).
有一平行板电容器,内部为真空,两个电极板间的间距为$\frac{L}{2}$,极板长为L,极板间有一匀强电场,U为两极板间的电压,电子从极板左端的正中央以初速v0射入,其方向平行于极板,并打在极板上,如图(甲)所示.电子的电荷量用e表示,质量用m表示,重力不计.回答下面问题(用字母表示结果). (1)“测定玻璃折射率”的实验中,在玻璃砖的一侧竖直插两个大头针A、B.在另一侧再竖直插两个大头针C、D,在插入第四个大头针D时,要使它挡住大头针D与大头针A、B的像,如图1在白纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边,根据该图用直尺画出光路图,并说明所要测量的物理量(用符号和文字说明)入射角i与折射角r,并据此写出求玻璃砖的折射率的表达式n=$\frac{sini}{sinr}$.
(1)“测定玻璃折射率”的实验中,在玻璃砖的一侧竖直插两个大头针A、B.在另一侧再竖直插两个大头针C、D,在插入第四个大头针D时,要使它挡住大头针D与大头针A、B的像,如图1在白纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边,根据该图用直尺画出光路图,并说明所要测量的物理量(用符号和文字说明)入射角i与折射角r,并据此写出求玻璃砖的折射率的表达式n=$\frac{sini}{sinr}$.
